
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 2.2.
Пример 2. 2.
Для условий примера 2. 1 составить характеристическое уравнение методом «входного сопротивления», найти его корни.
Решение
Метод «входного сопротивления» состоит в решении уравнения 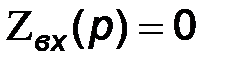 . Чтобы получить
. Чтобы получить 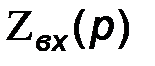 , необходимо в цепи после коммутации закоротить все источники эдс, разомкнуть все ветви, содержащие источники тока, а реактивные элементы при этом заменить следующим образом:
, необходимо в цепи после коммутации закоротить все источники эдс, разомкнуть все ветви, содержащие источники тока, а реактивные элементы при этом заменить следующим образом: 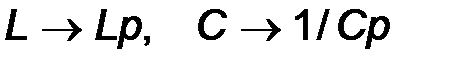 . Далее разрываем любую ветвь полученной цепи и определяем
. Далее разрываем любую ветвь полученной цепи и определяем 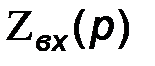 со стороны обрыва.
со стороны обрыва.
Запишем выражение для входного сопротивления цепи 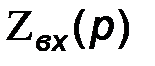 при размыкании первой ветви:
при размыкании первой ветви:
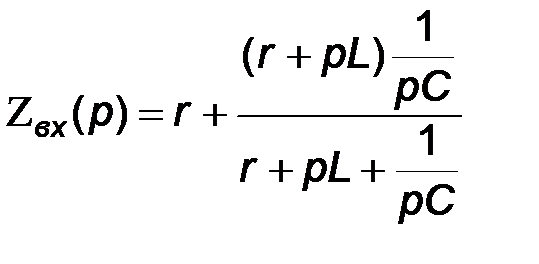 .
.
Составим характеристическое уравнение, полагая 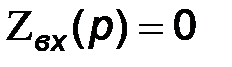 , т. е.
, т. е.
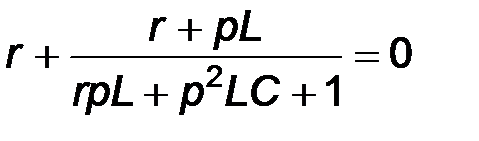 или
или 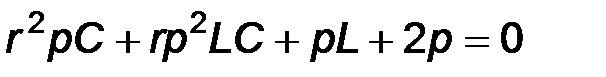 .
.
В приведенном виде
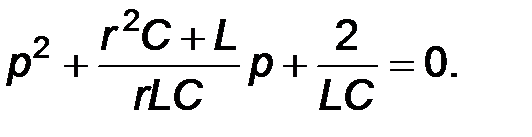
Сравнивая последнее уравнение и характеристическое уравнение в приведенном виде, полученное в примере 2. 1, можно сделать вывод, что независимо от того, какой метод используется для составления характеристического уравнения, итог будет один и тот же.
Следовательно, характеристическое уравнение имеет вид: 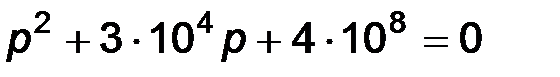 .
.
Решая квадратное уравнение, найдем корни характеристического уравнения
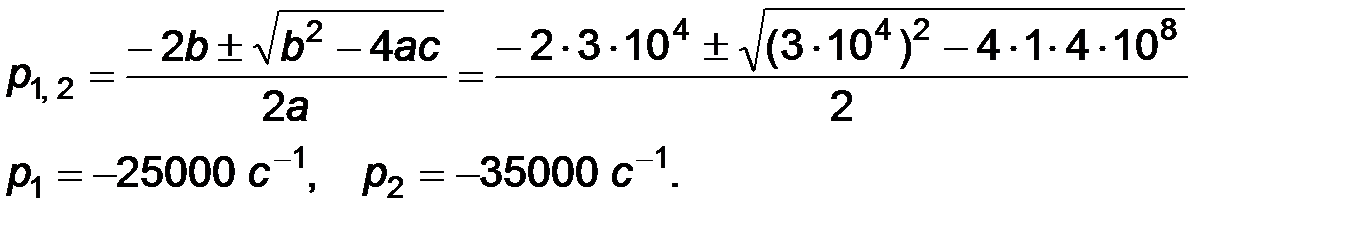 ,
,
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|