
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Модуль 4 Сызықты емес электрлік тізбектер
Практикалық сабақ №12
Сызық ты емес элементтері бар тармақ талмағ ан тізбектер
Сызық ты емес элементтері бар тармақ талмағ ан тізбектерді есептеудің графикалық ә дісі. Сызық ты емес элементтері бар тармақ талғ ан электр тізбектерін есептеу мысалдары.
Задача 6. 1. Зависимость u(t), показанная на рис. 6. 1, а и заданная табл. 6. 1 (для первой четверти периода), имеет симметрию относительно начала координат (нечетная) и относительно оси абсцисс при совмещении двух полупериодов: u(t) = -u(-t) = -u(t+T/2). Разложить зависимость u(t) в ряд Фурье и построить ее линейный спектр частот.
Таблица 6. 1. Значения функции u(t) для первой четверти периода
при Δ t = 0, 5 мс
| t, мс | 0, 5 | 1, 0 | 1, 5 | 2, 0 | 2, 5 | 3, 0 | 3, 5 | 4, 0 | 4, 5 | 5, 0 |
| un, В | 12, 35 | 17, 53 | 15, 89 | 16, 09 | 28, 15 | 54, 93 | 89, 78 | 121, 7 | 142, 7 | 149, 8 |
| n |
| -150 |
| -75 |
| мс |
| t |
| u |
| B |
| Рис. 6. 1 |
| а) |
| 2k-1 |
| um |
| B |
| б) |
Решение
Функция u(t) обладает одновременно двумя видами симметрии. Она нечетная и вместе с тем симметричная относительно оси абсцисс. Поэтому в ее разложении присутствуют только синусоиды с нечетным порядковым номером, а значение интеграла, определяющего амплитуду (2k–1)-ой гармоники, вычисляется за четверть периода с умножением результата на 4. Тогда значение амплитуды Um2k–1 определяется выражением:
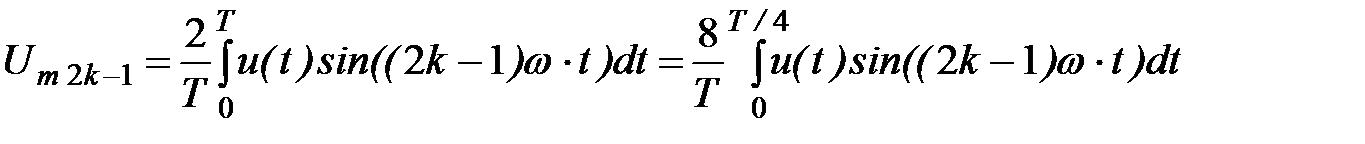 . (6. 1)
. (6. 1)
При использовании приближенного интегрирования период функции делится на равное число интервалов (в нашем случае их число N = 40) и производится замена dt = Т/N = Т/40. Однако, ввиду того, что значение функции определяется для конца интервала, и эти значения будут разными у двух симметричных интервалов, то с целью получения более точного результата за счёт компенсации положительной погрешности одного интервала отрицательной погрешностью симметричного интервала приближённое интегрирование должно выполняться за полпериода. Поэтому продолжим табл. 6. 1 до половины периода.
Продолжение таблицы 6. 1. Значения функции u(t) для второй четверти
периода при Δ t = 0, 5 мс
| t, мс | 5, 5 | 6, 0 | 6, 5 | 7, 0 | 7, 5 | 8, 0 | 8, 5 | 9, 0 | 9, 5 | 10, 0 |
| un, В | 142, 7 | 121, 7 | 89, 78 | 54, 93 | 28, 15 | 16, 09 | 15, 89 | 17, 53 | 12, 35 | |
| n |
Тогда последнее выражение (6. 1) приводится к виду (суммирование за половину периода):
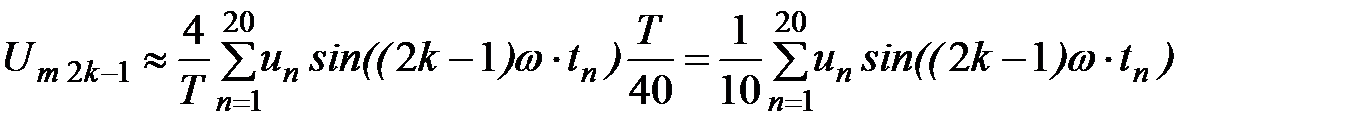 , (6. 2)
, (6. 2)
где Т = 0, 02 с – период функции u(t);
n = 1…20 – номер интервала приближенного интегрирования при Δ t = T/40.
Используя данные табл. 6. 1 и в соответствии с выражением (6. 2) выполнив расчетные действия для амплитуд первых 10 гармонических составляющих (учитывая только нечетные), получим:
Um1 = 100 В; Um3 = -40 В; Um5 = 15 В; Um7 = 5 В; Um9 = -0, 19 В.
Девятая гармоника, ввиду ее малости, может не учитываться в дальнейших действиях.
Определение мгновенного значения разложения функции u(t) в ряд Фурье (нечетные гармоники 1…9):
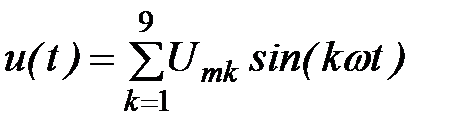 .
.
Примечание: выражение для u(t), записанное в более привычной “литературной“ форме имеет вид:
u(t) = 100sin(wt) – 40sin(3wt) + 15sin(5wt) + 5sin(7wt) – 0, 19sin(9wt).
Графики функции u(t) и амплитудного частотного спектра – на рис. 6. 1.
Задача 6. 2. Периодическое пилообразное напряжение, описываемое на интервале 0 < ω t< 2π функцией: u(ω t) = 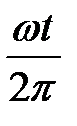 , представьте разложением в ряд Фурье.
, представьте разложением в ряд Фурье.
Решение
Постоянная составляющая (нулевая гармоника):
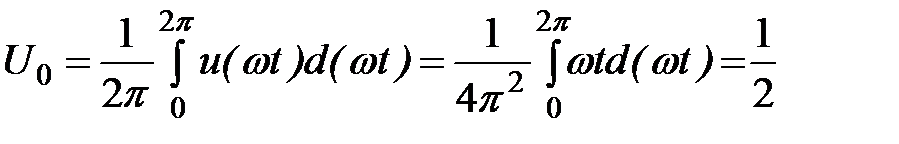 .
.
Кстати, она также находится из формулы для площади треугольника.
Коэффициенты синусных составляющих k-ой гармоники ряда Фурье определяются выражением:
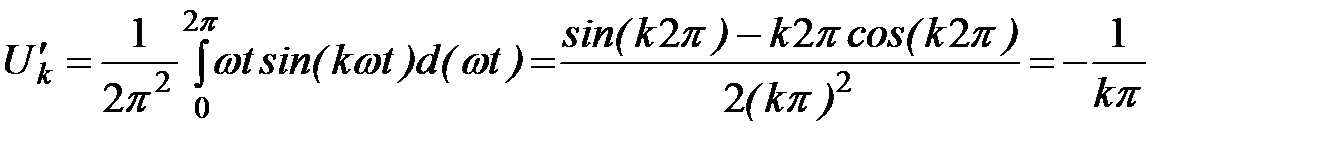 .
.
Аналогично для коэффициентов косинусных составляющих:
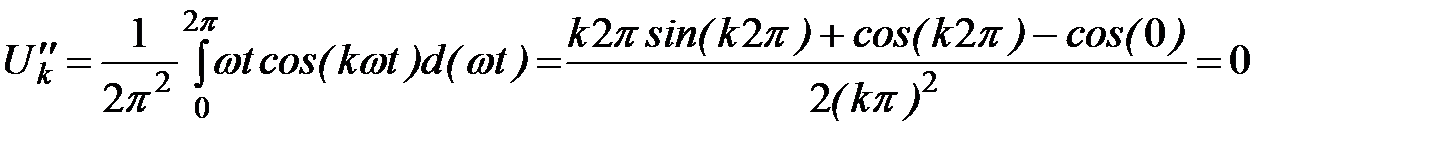 .
.
Таким образом, в разложении функции u(ω t) присутствуют только синусоидальные составляющие и разложение имеет вид:
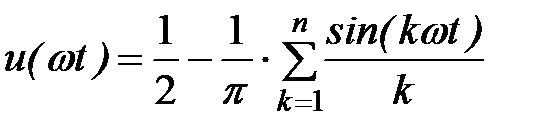 . (6. 3)
. (6. 3)
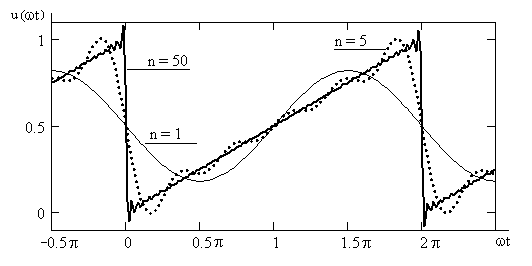
| Рис. 6. 2. Графики функции u(t). n = 1 – первая гармоника разложения (6. 3); n = 5 – сумма пяти гармо- ник разложения (6. 3); n = 50 – то же, сумма пятидесяти гармоник. |
На рис. 6. 2 приведены графики функции u(ω t), построенные в соответствии с (6. 3) для различного числа гармоник. Очевидно, что увеличение числа гармоник повышает точность представления исходной функции. Однако при этом всё в большей мере проявляются характерные “выбросы“ в точках разрыва исходной функции (явление Гиббса[1]). Это явление характерно тем, что функция, представленная тригонометрическим рядом, переходя через разрыв, делает скачок, превышающий исходную функцию примерно на 18%. Из-за явления Гиббса представление разрывных функций в окрестности
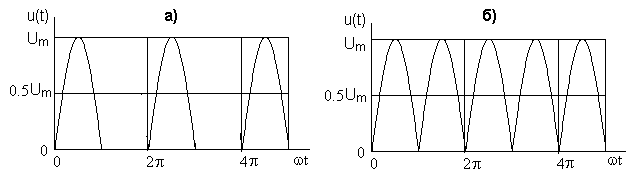
| Рис. 6. 3 |
Задача6. 3. Синусоидальное напряжение с амплитудой Um, у которого “срезаны“нижние полуволны (рис. 6. 3, а)[2], представить разложением в тригонометрический ряд.
Задача 6. 4. Напряжение на выходе однофазного мостового выпрямителя, описываемое функцией 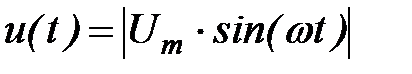 (рис. 6. 3, б), представить разложением в тригонометрический ряд.
(рис. 6. 3, б), представить разложением в тригонометрический ряд.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|