
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример решения задачи СТМ-1. Решение
Пример решения задачи СТМ-1
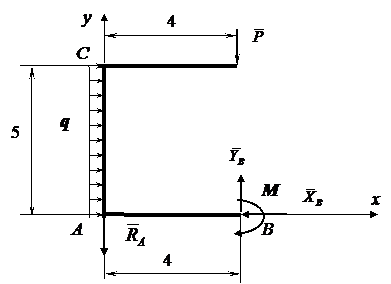
Построить эпюры продольных, поперечных сил и эпюру изгибающих моментов для рамы, показанной на рис 1. Для проверки построенных эпюр рассмотреть равновесие одного из узлов рамы. По заданному значению допускаемого напряжения [σ ]=1, 6·105 кПа подобрать двутавровое поперечное сечение рамы. Исходные данные для расчета:
l1=5 м, l2=4 м, M=10 кНм, P=15 кН, q=10 кН/м.
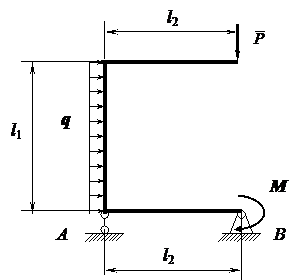 | |||
| |||
Решение
Расчет рамы выполняем в следующей последовательности:
1. Определение опорных реакций;
2. Определение внутренних усилий в элементах рамы и построение эпюр N, Q, M;
3. Проверка правильности построения эпюр;
4. Расчет требуемых размеров поперечного сечения рамы по заданным допускаемым напряжениям.
1. Определение опорных реакций
Опора A – шарнирная подвижная, ее реакцию 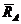 направим вдоль опорного стержня вверх (рис. 2); опора В – шарнирно неподвижная, ее реакцию представим в виде двух составляющих
направим вдоль опорного стержня вверх (рис. 2); опора В – шарнирно неподвижная, ее реакцию представим в виде двух составляющих 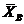 и
и 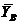 . Сами опоры можно не изображать на расчетной схеме, поскольку справедлив принцип освобождаемости от связей, известный из раздела «Статика» курса теоретической механики: «Всякое тело можно рассматривать как свободное, если действие связей заменить их реакциями».
. Сами опоры можно не изображать на расчетной схеме, поскольку справедлив принцип освобождаемости от связей, известный из раздела «Статика» курса теоретической механики: «Всякое тело можно рассматривать как свободное, если действие связей заменить их реакциями».
Полученная система сил - произвольная плоская, аналитические условия равновесия которой имеют вид:
1. 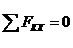 ; 2.
; 2. 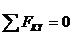 ; 3.
; 3. 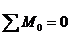 . (1)
. (1)
В этих формулах для сокращения записи не указываем пределы суммирования, понимая, что суммирование выполняется для всех приложенных сил и пар сил. Индекс O у момента в 3-м уравнении напоминает, что это уравнение можно составлять относительно любой точки, но предпочтительно выбирать точку, через которую проходит возможно большее число неизвестных сил (из алгебраических соображений, для получения наиболее простого уравнения). Таких точек в этой задаче две: А и В. Принимаем точку А и составляем уравнения
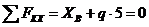 ; (2)
; (2)
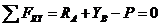 ; (3)
; (3)
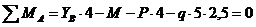 . (4)
. (4)
 |
Из уравнения (4) находим 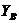
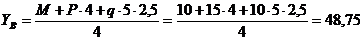 кН,
кН,
затем из уравнений (3) и (2) находим  и
и  .
.
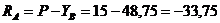 кН;
кН;
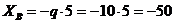 кН.
кН.
Найденные значения опорных реакции необходимо проверить, для этого составим сумму моментов всех действующих на раму сил ( в том числе и найденных реакций) относительно любой точки (теперь предпочтительно выбрать точку, через которую не проходят проверяемые реакции связей, иначе мы их не проверим, т. к. их моменты будут равны нулю). Составим это уравнение относительно точки D (рис. 2).
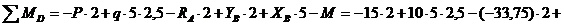
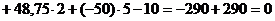 ,
,
следовательно, реакции опор определены правильно. Иногда из-за погрешностей расчетов может получиться, что  . Погрешность
. Погрешность  допустима, если не превышает 3% от минимального по модулю проверяемого значения, т. е. в данном примере
допустима, если не превышает 3% от минимального по модулю проверяемого значения, т. е. в данном примере 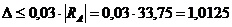 кНм.
кНм.
Реакции 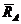 и
и 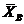 получились по расчету отрицательными, значит их действительное направление противоположно принятому. Показываем их истинное направление (опоры можно не показывать, т. к. главный вектор и главный момент всех действующих на раму внешних сил (рис. 3) равны нулю и рама находится в равновесии при действии показанных сил) и переходим к определению главных векторов и главных моментов внутренних сил в характерных сечениях рамы.
получились по расчету отрицательными, значит их действительное направление противоположно принятому. Показываем их истинное направление (опоры можно не показывать, т. к. главный вектор и главный момент всех действующих на раму внешних сил (рис. 3) равны нулю и рама находится в равновесии при действии показанных сил) и переходим к определению главных векторов и главных моментов внутренних сил в характерных сечениях рамы.
 | |||
| |||
2. Определение внутренних усилий в поперечных сечениях рамы
и построение эпюр N, Q, M.
Для определения внутренних усилий в поперечных сечениях любой конструкции необходимо мысленно ее рассекать в характерных сечениях, показывать направления главного вектора и главного момента внутренних сил и рассматривать равновесие одной из отсеченных частей конструкции. Главный вектор и главный момент внутренних сил прикладываются в центре тяжести сделанного сечения рамы и называются N и Q – продольная и поперечная составляющие главного вектора, соответственно, продольной и поперечной силой, главный момент М внутренних сил – изгибающим моментом в поперечном сечении конструкции. Напомним, что при действии на такую раму пространственной внешней системы сил в поперечных сечениях рамы возникали бы пространственные системы внутренних сил и их главные векторы и главные моменты раскладывались бы на 3 составляюших: N, Q1, Q2 – составляющие главного вектора, M1, M2, Mкр – составляющие главного момента. Они имеют следующие названия: N –продольная сила, Q1, Q2 – поперечные силы, направленные вдоль главных центральных осей рассматриваемого поперечного сечения,
M1, M2 – изгибающие моменты относительно указанных осей и Mкр – крутящий момент, направленный вдоль продольной оси.
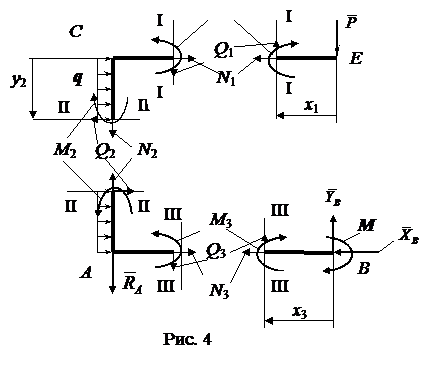
Характерных участков в рассматриваемой раме 3: верхний ригель СЕ, стойка СА, нижний ригель АВ. Напомним, что характерными называются участки конструкции, в пределах которых закономерности изменения внешних нагрузок и жесткостных параметров по длине рассматриваемого участка рамы остаются неизменными. В нашем случае все элементы рамы будут изготовлены из одного стандартного профиля, поэтому жесткостные параметры по длине рамы остаются постоянными. Что касается внешней нагрузки, то необходимо рассмотреть каждый из трех участков. На ригеле СЕ в точке Е приложена сила Р1, мысленно рассекая раму в любом месте ригеля (рис. 4) слева и справа от сечения I-I будем иметь неизменные системы внешних сил. Аналогичные рассуждения можем сделать о системах внешних сил, расположенных по двум сторонам относительно сечений II-II и III-III рамы (рис. 4).
|
Правило знаков для изгибающих моментов в курсе сопротивления материалов связано со знаком кривизны изогнутой продольной оси балки в принятой системе координатных осей. В курсе строительной механики элементы конструкции могут иметь разное положение (горизонтальное, вертикальное, наклонное), поэтому определенного правила знаков для изгибающих моментов нет. Есть правило откладывать значения изгибающих моментов при построении эпюр на стороне растянутых волокон. Поэтому направляем изгибающие моменты М1, М2, М3 в сечениях рамы произвольно (рис. 4), как реакции внешних связей на первом этапе решения задачи, а угадали мы их действительное направление или нет, покажет их знак при решении условий равновесия сил, приложенных к мысленно отсеченной части конструкции. При направлении внутренних усилий по обе стороны от сделанных сечений конструкции помним о III законе Ньютона и направляем их в противоположные стороны (рис. 4).
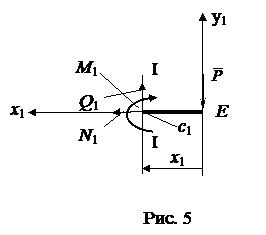
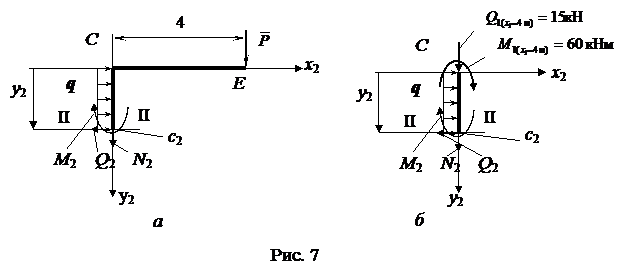
Рассмотрим участок ригеля СЕ рамы (рис. 5), в сечении I-I показываем определяемые внутренние усилия N1, Q1, направляем их в положительном направлении, и главный момент внутренних сил (изгибающий момент) M1, который направляем произвольно. Координата сечения обозначена x1 (0 ≤ x1 ≤ 4 м), центр тяжести поперечного сечения рамы обозначен с1, именно в нем и приложены главный векторй и главный момент внутренних сил N1, Q1, M1. Показана локальная система координат x1-y1, в которой будем составлять аналитические условия равновесия рассматриваемой системы сил:
1)  ,
,  (const по длине ригеля СЕ );
(const по длине ригеля СЕ );
2) 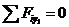 ,
, 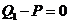 ,
, 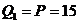 кН (const по длине ригеля СЕ );
кН (const по длине ригеля СЕ );
3) 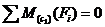 ,
, 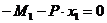 ,
,
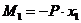 - линейная зависимость,
- линейная зависимость,
при 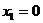
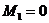 ,
,
при 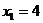 м
м 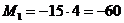 кНм.
кНм.
Знак минус у 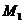 говорит о том, что мы не угадали его направление, действительное направление
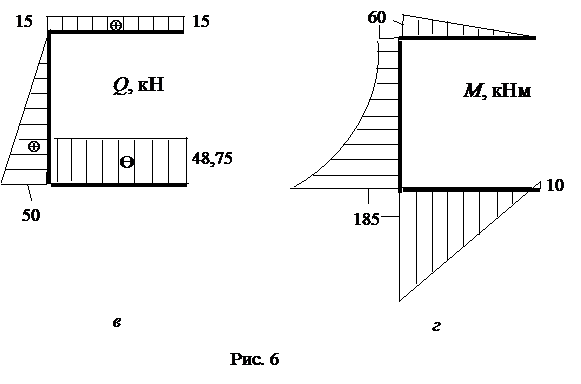
говорит о том, что мы не угадали его направление, действительное направление 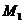 противоположно показанному на рис. 5 и, следовательно, растянутые волокна на ригеле СЕ будут верхние. Это учитываем при построении эпюры М (рис. 6, г), которая стороится со стороны растянутых волокон. Откладываем полученные значения N1 и Q1 на ригеле СЕ на эпюрах N и Q (рис. 6, а, б, в). На этих эпюрах указывают знаки N и Q, поэтому не принципиально где откладывать положительные их значения, а где отрицательные, для демонстрации этого показаны две эпюры N (рис. 6, а, б).
противоположно показанному на рис. 5 и, следовательно, растянутые волокна на ригеле СЕ будут верхние. Это учитываем при построении эпюры М (рис. 6, г), которая стороится со стороны растянутых волокон. Откладываем полученные значения N1 и Q1 на ригеле СЕ на эпюрах N и Q (рис. 6, а, б, в). На этих эпюрах указывают знаки N и Q, поэтому не принципиально где откладывать положительные их значения, а где отрицательные, для демонстрации этого показаны две эпюры N (рис. 6, а, б).
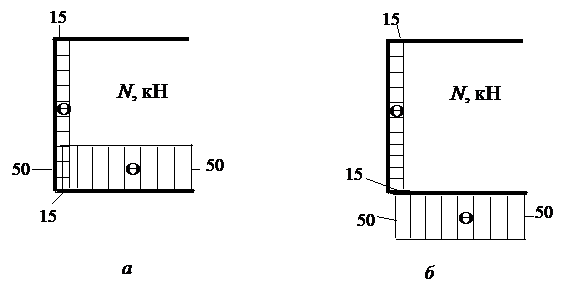 | |||
 | |||
Рассмотрим участок стойки СА рамы с ригелем (рис. 7, a), т. е. всю верхнюю относительно сечения II-II отсеченную часть рамы. В сечении показываем определяемые внутренние усилия N2, Q2, направляем их в положительном направлении, и главный момент внутренних сил (изгибающий момент) M2, который направляем произвольно. Координата сечения обозначена y2 (0 ≤ y2 ≤ 5 м), центр тяжести поперечного сечения рамы обозначен с2, именно в нем и приложены главный вектор и главный момент внутренних сил N2, Q2, M2. Показана локальная система координат x2-y2, в которой будем составлять аналитические условия равновесия рассматриваемой системы сил:
 |
1) 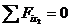 ,
, 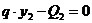 , откуда
, откуда 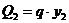 , (линейная зависимость),
, (линейная зависимость),
при 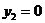
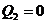 , при
, при 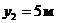
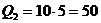 кН.
кН.
2) 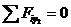 ,
, 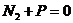 ,
, 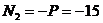 кН (const по длине стойки СА );
кН (const по длине стойки СА );
3) 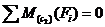 ,
, 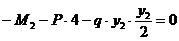 , откуда
, откуда
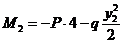 уравнение квадратной параболы, которую можно провести на эпюре М через две точки. Для этого вычисляем:
уравнение квадратной параболы, которую можно провести на эпюре М через две точки. Для этого вычисляем:
при 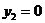
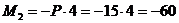 кНм; при
кНм; при 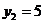 м
м 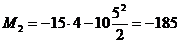 кНм.
кНм.
Получены значения М2 со знаком минус, т. е. мы не угадали его направления. Реальные направления изгибающего момента в стойке СА противоположны показанному на рис. 7, а, что означает, что растянутые волокна в стойке будут не справа, а слева от продольной оси стойки. Откладываем эти значения на левой стороне стойки (см. рис. 6, г ) и соединяем их кривой с выпуклостью в направлении q. Это объясняется зависимостью Журавского Д. И. между характерами изменения изгибающего момента 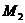 и поперечной силы
и поперечной силы 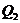 вдоль оси
вдоль оси 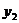
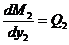 .
.
Вспоминаем геометрический смысл производной – это 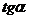 – угла наклона касательной к эпюре
– угла наклона касательной к эпюре 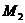 и осью
и осью 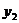 . При
. При 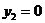
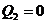 ,
, 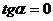 ,
, 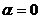 , а далее с ростом
, а далее с ростом 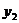 увеличиваются
увеличиваются 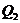 и
и 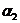 .
.
Для тех, кто испытывает затруднение с применением зависимости Журавского Д. И., можем порекомендовать вычислить значение изгибающего момента 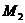 еще в одной промежуточной точке (например, при
еще в одной промежуточной точке (например, при 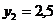 м) и затем провести параболу
м) и затем провести параболу 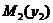 через три точки.
через три точки.
На рис. 7, б показана еще одна расчетная схема для определения внутренних усилий в стойке СА. Показан только отрезок стойки длиной 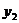 , но воздействие «отброшенного» ригеля СЕ на стойку изображено внутренними усилиями
, но воздействие «отброшенного» ригеля СЕ на стойку изображено внутренними усилиями
в сечении ригеля с координатой 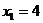 м
м 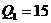 кН и
кН и 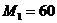 кНм,
кНм,  , но с учетом III закона Ньютона, поскольку эти усилия приложены не к ригелю, а к стойке (см. рис. 4).
, но с учетом III закона Ньютона, поскольку эти усилия приложены не к ригелю, а к стойке (см. рис. 4).
Составляем условия равновесия сил, показанных на этой расчетной схеме:
1) 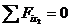 ,
, 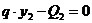 , откуда
, откуда 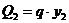 , (линейная зависимость),
, (линейная зависимость),
при 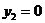
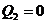 , при
, при 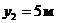
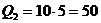 кН.
кН.
2) 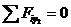 ,
, 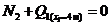 ,
, 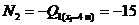 кН (const по длине стойки СА );
кН (const по длине стойки СА );
3) 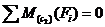 ,
, 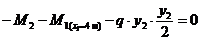 , откуда
, откуда
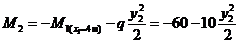 , что совпадает с ранее полученным уравнением квадратной параболы.
, что совпадает с ранее полученным уравнением квадратной параболы.
Рассмотрим участок нижнего ригеля рамы (рис. 8), удобно изучать равновесие правой относительно сечения III-III отсеченной части рамы (см. рис. 4). В сечении III-III показываем определяемые внутренние усилия N3, Q3, направляем их в положительном направлении, и главный момент внутренних сил (изгибающий момент) M3 который направляем произвольно. Координата сечения обозначена x3 (0 ≤ x3 ≤ 4 м), центр тяжести поперечного сечения рамы обозначен с3, в нем приложены главный вектор и главный момент внутренних сил N3, Q3, M3. Показана локальная система координат x3-y3, в которой будем составлять аналитические условия равновесия рассматриваемой системы сил:
1)  ,
, 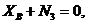
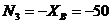 кН, (const по длине ригеля).
кН, (const по длине ригеля).
2) 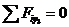 ,
, 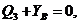
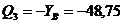 кН, (const по длине ригеля).
кН, (const по длине ригеля).
3) 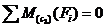 ,
, 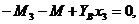
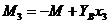 , (линейная зависимость). При
, (линейная зависимость). При 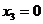
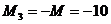 кНм, при
кНм, при 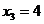 м
м 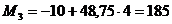 кНм.
кНм.
Чтобы правильно отложить на эпюре М (рис. 6, г), нужно помнить, что эта эпюра строится на стороне растянутых волокон изучаемого элемента рамы. При 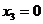
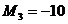 кНм, т. е.
кНм, т. е. 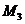 направлено не так, как мы предполагали на рис. 8, а в противоположную сторону, а это значит, что растянутыми будут верхние волокна ригеля, откладываем на эпюре М (рис. 6, г) 10 кНм сверху. При
направлено не так, как мы предполагали на рис. 8, а в противоположную сторону, а это значит, что растянутыми будут верхние волокна ригеля, откладываем на эпюре М (рис. 6, г) 10 кНм сверху. При 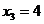 м
м 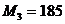 кНм. Значение
кНм. Значение 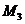 получено со знаком плюс, это значит, что его наравление совпадает с принятым на рис. 8 и растянутыми будут нижние волокна ригеля. Откладываем значение
получено со знаком плюс, это значит, что его наравление совпадает с принятым на рис. 8 и растянутыми будут нижние волокна ригеля. Откладываем значение 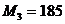 кНм снизу ригеля на эпюре М (рис. 6, г).
кНм снизу ригеля на эпюре М (рис. 6, г).
3. Проверка правильности построения эпюр внутренних сил.
Проверку выполняем рассмотрением равновесия каждого узла рамы под действием найденных внутренних усилий.
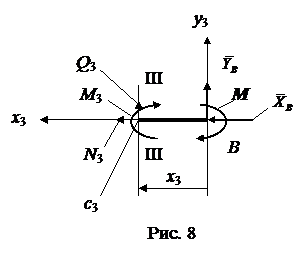
Вырезаем узел С. Внешних нагрузок к этому узлу не приложено, но найденные внутренние усилия в примыкающих к узлу эпементах (ригеле CE и стойке СА) необходимо изобразить как внешние силы (рис. 9).
В ригеле СЕ (рис. 6) продольная сила 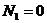 , поперечная сила
, поперечная сила  , знак плюс означает, что
, знак плюс означает, что 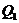 поворачивает отсеченный элемент конструкции по ходу часовой стрелки, что и отражено на рис. 9.
поворачивает отсеченный элемент конструкции по ходу часовой стрелки, что и отражено на рис. 9.
В стойке СА поперечная сила равна нулю, продольная сила отрицательна, т. е. стойка испытывает сжатие, поэтому направляем силу  к узлу С.
к узлу С.
Эпюра изгибающих моментов строится со стороны растянутых волокон элементов конструкции (рис. 6, г), в соответствии с этим правилом направляем моменты 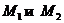 на рис. 9.
на рис. 9.
Составляем условия равновесия системы сил, изображенных на рис. 9. 1.  ,
,
2. 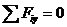 ,
, 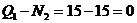 .
.
3. 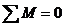 ,
, 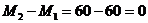 .
.
В последнем уравнении мы даже не указываем относительно какой точки составляется это уравнение, поскольку размеры вырезанного узла бесконечно малы и моменты всех сил (  ) относительно точки С равны нулю, в уравнении 3 учитываются только моменты пар сил, к которым приводятся главные моменты внутренних сил в поперечных сечениях ригеля и стойки. Помним из раздела «Статика» курса теоретической механики теорему: «Сумма моментов сил, образовавших пару, относительно любой точки равна моменту пары».
) относительно точки С равны нулю, в уравнении 3 учитываются только моменты пар сил, к которым приводятся главные моменты внутренних сил в поперечных сечениях ригеля и стойки. Помним из раздела «Статика» курса теоретической механики теорему: «Сумма моментов сил, образовавших пару, относительно любой точки равна моменту пары».
Уравнения равновесия выполняются, следовательно узел С находится в равновесии.
По условию задания достаточно рассмотреть равновесие одного узла рамы. Но здесь мы рассмотрим еще равновесие узла А. Характерной особенностью является внешняя реакция опоры  , приложенная к этому узлу (см. рис. 3). Расчетная схема показана на рис. 10.
, приложенная к этому узлу (см. рис. 3). Расчетная схема показана на рис. 10.
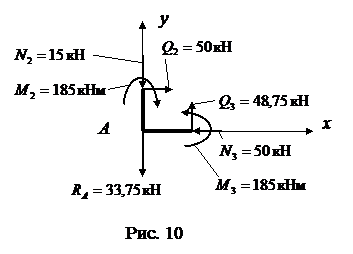 |
Составляем условия равновесия системы сил, изображенных на рис. 10. 1.  ,
, 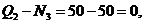
2. 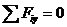 ,
, 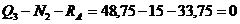 ,
,
3. 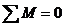 ,
, 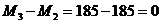 .
.
Условия равновесия выполняются, следовательно, єпюры внутренних усилий построены правильно.
4. Расчет требуемых размеров поперечного сечения рамы
Из условия прочности 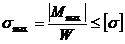 находим требуемое значение момента сопротивления поперечного сечения рамы
находим требуемое значение момента сопротивления поперечного сечения рамы
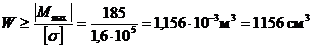 .
.
По таблице сортаментов прокатных профилей «Балки двутавровые» [2] выбираем двутавр с ближайшим большим значением момента сопротивления, это двутавр N45 c Wx=1231 см3.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|