Примеры. Геометрический смысл производной.

Примеры. Геометрический смысл производной.

1. Задание. Прямая 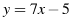параллельна касательной к графику функции 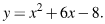Найдите абсциссу точки касания.

Решение.

Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой 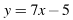их угловые коэффициенты равны. Поэтому абсцисса точки касания находится из уравнения :

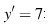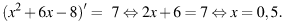
Ответ: 0, 5.

2. Задание. Прямая 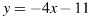является касательной к графику функции 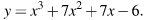Найдите абсциссу точки касания.

Решение.

Условие касания графика функции 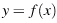и прямой 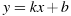задаётся системой требований:

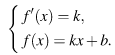
В нашем случае имеем:

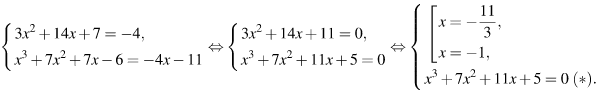
Проверка подстановкой показывает, что первый корень не удовлетворяет, а второй удовлетворяет уравнению (*). Поэтому искомая абсцисса точки касания − 1.

Ответ: − 1.