«Российский государственный геологоразведочный университет имени

МИНОБРНАУКИ РОССИИ

СТАРООСКОЛЬСКИЙ ФИЛИАЛ

ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«Российский государственный геологоразведочный университет имени

Серго Орджоникидзе»

СОФ МГРИ – РГГРУ

Кафедра «Горного дела, экологии и природопользования»

КУРСОВой проект

ПОСТРОЕНИЕ ОТКОСОВ ВЫЕМКИ И НАСЫПИ

ЗЕМЛЯНОГО СООРУЖЕНИЯ

по дисциплине «Начертательная геометрия, инженерная и компьютерная графика»

Выполнил:

студент гр. _____ < подпись> И. О. Ф.

Руководитель:

________ ________ < подпись> И. О. Ф.

«___» __________ 201__ г.

Старый Оскол

СОДЕРЖАНИЕ

Введение 3

1. Исходные данные 3

2. Правила выполнения построений и оформления 6

3. Сущность метода проекций с числовыми отметками 9

3. 1. Прямая линия в проекциях с числовыми отметками 10

3. 2. Уклон и заложение прямой 10

3. 3. Плоскость в проекциях с числовыми отметками 12

3. 3. 1. Пересечение плоскостей между собой 15

3. 4. Топографическая поверхность 16

3. 5. Пересечение топографической поверхности с плоскостью 17

4. Определение границ выемки и насыпи земляного сооружения 18

5. Построение геологического профиля 20

Заключение 21

Список использованных источников 22

Введение

Курсовой проект является заключительным этапом изучения дисциплины и предназначен для закрепления практических навыков самостоятельного решения инженерно-геологических задач.

С этой целью, предстоит выполнить две задачи, связанные с определением границ земляных работ при возведении земляного сооружения в проекциях с числовыми отметками, и построение профиля земляного сооружения.

Как известно, горно-геологические объекты (геологические тела, горные выработки, буровые скважины и т. д. ) в подавляющем большинстве случаев имеют сложнейшее пространственное строение. Точно отобразить эти объекты на чертеже со всеми их геологическими особенностями почти невозможно. Поэтому инженер – геолог должен уметь не только представлять себе положение их в пространстве, но и при отображении на бумажном носителе уметь упрощать, моделировать, приводить к более или менее простым геометрическим телам, не внося при этом существенных погрешностей в форму и размеры изображаемого объекта.

Сама по себе это уже достаточно сложная позиционная задача и ее успешное решение требует определенных навыков и инженерной интуиции. Во многих случаях ее решение требует привлечения компьютеров и компьютерных технологий.

В практику инженерной деятельности, в том числе в геологической отрасли, все шире внедряются компьютеры, и горный инженер-геолог должен владеть методами компьютерной графики.

Курсовой проект представляет собой комплексное задание, содержащее все основные элементы теоретического курса. При выполнении проекта закрепляются полученные теоретические знания и приобретаются практические навыки самостоятельного решения сравнительно сложных инженерно-геологических задач графическими методами.

1 Исходные данные

Дана топографическая поверхность на участке 40х40 м² (рис. 1), заданная горизонталями, и земляное сооружение (рис. 2) с указанными уклонами откосов выемки, насыпи и дороги. Откосы выемок имеют уклон 1: 1, откосы насыпей – 1: 1, 5 и уклон дороги – 1: 6 (рис. 3).

Требуется: 1 – построить линию пересечения откосов выемок и насыпей земляного сооружения (площадки и дороги) с топографической поверхностью и между собой.

2 – построить профиль земляного сооружения по сечению вертикальной плоскостью Е-Е.

Для выполнения задания на формате А3 перечерчиваем в масштабе 1: 200 план земельного участка, рельеф которого задан горизонталями и наносим на него в том же масштабе план земляного сооружения так, чтобы центр сооружения (точка О) совпал с центром участка. Откладываем азимут (ось сооружения наклонена к меридиану под заданным углом) 0 градусов. Отметка площадки земляного сооружения + 22, 000 метра. Соответственно, линия нулевых работ на площадке будет проходить по горизонтали с отметкой 22 метра.

Топографическая поверхность с горизонталями и размещенной площадкой земляного сооружения приведена на рис. 4.

Горизонтали топографической поверхности

(1: 100)

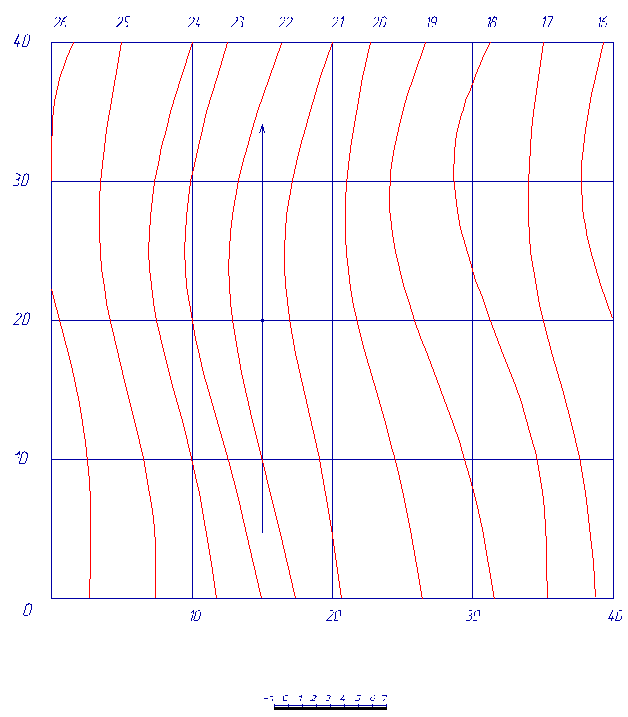
Рис. 1

Земляное сооружение

(1: 100)

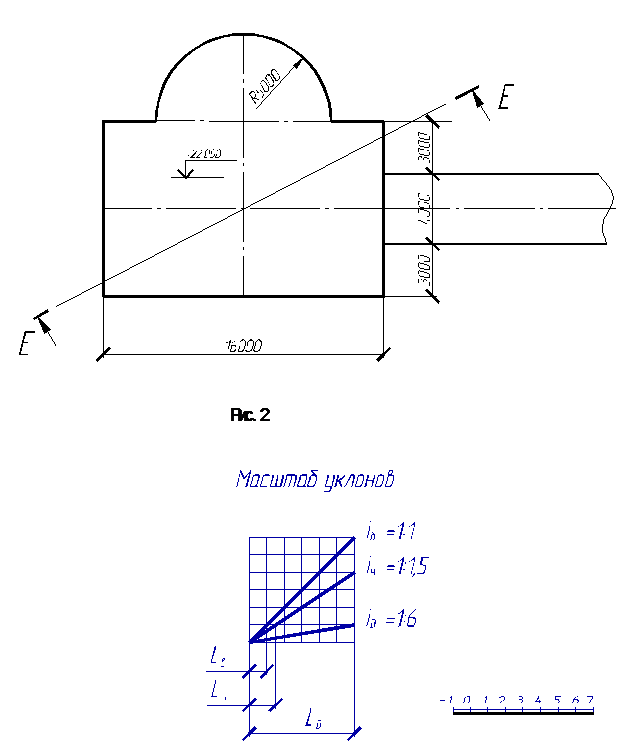
Рис. 3

Горизонтали топографической поверхности и земляное сооружение

(1: 100)

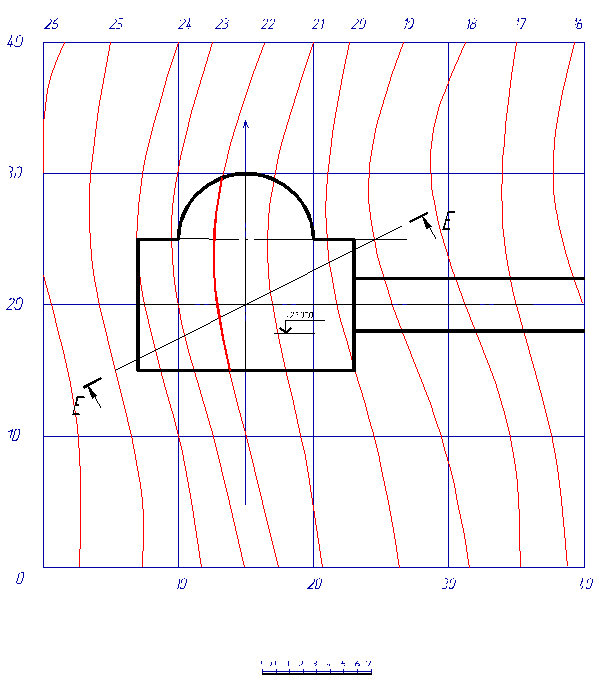
Рис. 4

2. Правила выполнения построений и оформления

Курсовой проект выполнен с использованием прикладного пакета AutoCAD 2015. Для удобства работы при выполнении построений откосов выемки и насыпи горизонтали топографической поверхности и разбивочную сетку участка разместили на заблокированном слое, что исключает возможность их несанкционированного изменения.

Контур земляного сооружения и линии пересечения откосов с топографической поверхностью и между собой задавали толщиной 0, 6 мм.

Штриховку откосов выемок и насыпей задавали толщиной 0, 1…0, 2 мм перпендикулярно проектным горизонталям откосов при расстоянии между штрихами 1, 5…2, 5 мм. Линии построения, в том числе проектные горизонтали, задавали также толщиной 0, 1…0, 2 мм.

Для построения горизонталей откосов выемки, насыпи и дороги при помощи масштаба уклонов определили величину интервала.

Интервал для откосов выемки, при выполнении построений в масштабе 1: 200, составил 5 мм. Интервал откосов насыпей – 7, 5 мм. Интервал откосов дороги – 30 мм. Масштаб уклонов приведен ранее на рис. 3.

Интервалы откосов выемки наносим на масштабы уклонов всех элементов (плоскостей) откосов и проводим горизонтали перпендикулярно масштабам уклонов, как показано на рис. 5. Аналогичные построения выполняем для откосов насыпи (рис. 6) и дороги (рис. 7).

Выемка грунта на проектируемой площадке производится слева от линии нулевых работ. Соответственно насыпь на проектируемой площадке располагается справа от линии нулевых работ.

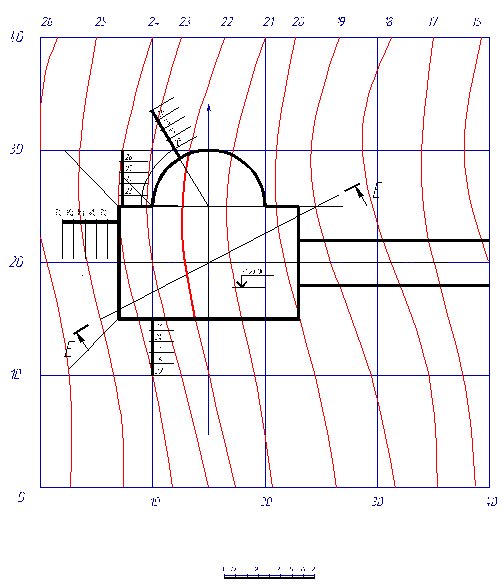
Рис. 5

Горизонтали и масштаб уклонов насыпи

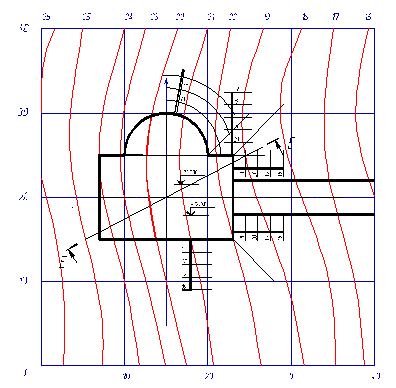
Рис. 6

Горизонтали и масштаб уклонов дороги

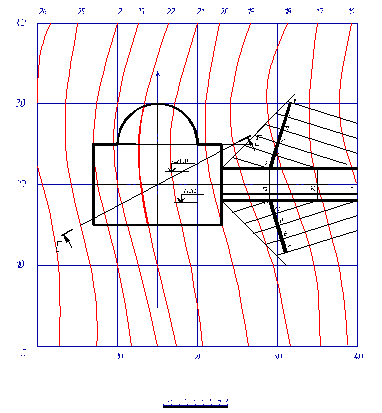
Рис. 7

3 Сущность метода проекций с числовыми отметками

В прямоугольных проекциях предмет проецируют на две или три плоскости проекций.

Но, если вертикальные размеры изображаемого предмета существенно невелики по сравнению с горизонтальными (длиной и шириной), то построение фронтальной проекции затруднено, а практическое ее использование неудобно. В таком случае пользуются особым методом построения изображений, называемым методом проекций с числовыми отметками. Наибольшее применение этот метод нашел в решении задач при горном и геологоразведочном производстве.

Проекции с числовыми отметками были впервые применены для изображения на морских картах глубины в различных пунктах водных бассейнов. В XVI веке был предложен способ изображения топографической поверхности кривыми линиями, которые соединяли целый ряд точек, лежащих на одном уровне. Данные кривые линии получили название горизонталей.

Сущность метода проекций с числовыми отметками заключается в следующем. Изображаемый предмет прямоугольно проецируют только на одну горизонтально расположенную плоскость проекций П₀, называемую плоскостью нулевого уровня.

На чертеже в этом случае отображаются только два его измерения: длина и ширина. Третье измерение – высота изображаемого предмета – выражается числами, определяющими расстояние от точек предмета до плоскости проекций.

Эти числа называют числовыми отметками. Плоскость проекций П₀, относительно которой ориентируют точки пространства, называют основной или плоскостью нулевого уровня. В решении географических, геодезических геологических задач за такую плоскость принимают уровень воды моря и океана. В России все абсолютные высоты отсчитываются от нуля Кронштадтского футштока. Изображение в проекциях с числовыми отметками называется планом (рис. 8).

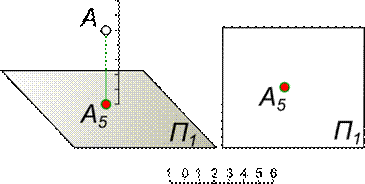
Рис. 8

Для полного определения пространственного расположения изображенных на чертеже точек необходимо наличие масштаба (масштаб всегда указывается на чертеже) и указания линейной единицы, в которой выражены числовые отметки.

Например, точка А₅ на плане имеет две координаты Х и У, а ее высота от нулевой плоскости будет равна 5 масштабным единицам.

3. 1. Прямая линия в проекциях с числовыми отметками

В зависимости от расположения относительно плоскости проекций различают три вида прямых: наклонные, горизонтальные и вертикальные.

Проецирование наклонной прямой АВ в проекциях с числовыми отметками. Прямая АВ, расположенная в пространстве произвольно, на чертеже имеет проекцию - прямую линию, которая соединяет проекцию точки А - А₁ и проекцию точки В - В₆. Проекция А₁В₆ соответствует только одному положению прямой в пространстве, при условии, что задан масштаб чертежа (Рис. 9). Угол наклона прямой АВ к горизонтальной плоскости является угол между отрезком прямой АВ и ее проекцией. Если крайние точки отрезка прямой имеют одинаковые отметки, например А₈В₈, это означает что прямая горизонтальная. Фронтальная проекция такой прямой, построенной с помощью линий связи будет параллельна оси проекций.

Проецирование прямой АВ в проекциях с числовыми отметками, позволяет найти натуральную величину отрезка.

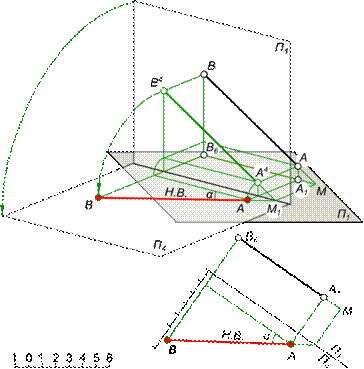
Рис. 9

Проецируем прямую АВ на вспомогательную вертикальную плоскость П₄, совмещаемую затем с горизонтальной плоскостью П₁. Плоскость П₄ также параллельна прямой АВ, вследствие чего прямая АВ проецируется на нее в натуральную величину. Угол наклона прямой к плоскости П₁ - угол между отрезком АВ и его проекцией (Рис. 9).

3. 2. Уклон и заложение прямой

В проекциях с числовыми отметками для задания прямой необходимо указать направление проекции, или отметки одной из ее точек, или уклон и интервал. Стрелка указывает направление понижения отметок.

Заложение прямой - это длина проекции данной прямой, обозначаемая L.

Уклон прямой - это отношение разности высотных отметок концов прямой к заложению прямой: i = (h1 - h)/L = tgα.

Интервал прямой - это горизонтальная проекция отрезка между двумя точками прямой, имеющими разность уровней в одну единицу (Рис. 10).:

l = O/(h1 - h) = ctgα.

Так как ctgα = 1/tgα, то l = 1/i то есть уклон и интервал - величины обратные друг другу.

В частном случае: - если прямая линия горизонтальна, угол α =0 и i=0, интервал l=1/i=∞; - если прямая линия вертикальна, угол α =90° тогда i=∞, интервал l=1/i=0.

Уклон откосов выемок и насыпей задается отношением, например: 1: 2, 1: 3; или в процентах - 10%, 20%; или в промиллях - 20%, 50% для уклонов вдоль дорог и каналов. Промилле - одна тысячная какого-либо числа, десятая часть процента.

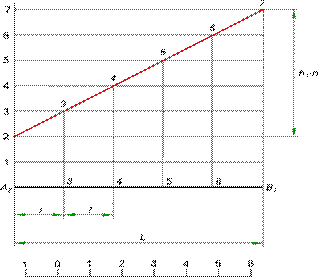
Рис. 10

У наклонной прямой различают два направления: направление падения и противоположное ему направление восстания. Каждое из направлений с северным направлением меридиана составляет на плане угол, который носит название азимута.

Угол b ( азимут ) отсчитывают по ходу часовой стрелки.

В горно-геологической практике, помимо перечисленных выше двух способов, используется задание прямой ее элементами залегания: точкой, азимутом падения и углом наклона прямой к плоскости проекций, который носит название угла падения прямой. Под азимутом падения понимают правый угол, составленный на плане северным направлением меридиана и направлением падения прямой.

У горизонтальной прямой различают два направления, которые носят название направлений простирания. На плане с северным направлением меридиан они составляют углы, которые называют азимутами простирания. Под азимутом простирания понимают правый угол, составленный на плане северным направлением меридиана и одним из направлений простирания прямой.

Определение на проекции прямой точек, отметки которых имеют постоянную разность, называют интерполированием (градуированием) прямой. Интерполирование прямой на плане сводится к определению заложения прямой, соответствующего заданной высоте сечения. Если прямая задана двумя точками, то длина отрезка, соединяющего их проекции, будет заложением прямой для высоты сечения, равной разности числовых отметок этих точек.

3. 3. Плоскость в проекциях с числовыми отметками

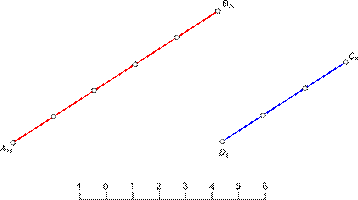
Проецирование плоскости в проекциях с числовыми отметками может быть выполнено (рис. 11):

- проекциями трех точек, не лежащих на одной прямой;

- проекциями двух параллельных прямых;

или

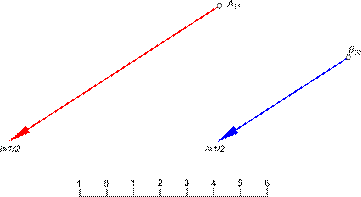
- проекциями двух пересекающихся прямых AB и EF.

Рис. 11

Угол падения плоскости в проекциях с числовыми отметками - это угол между линией ската плоскости и ее проекцией. Также этот угол называют углом наибольшего ската плоскости (Рис. 12).

Рис. 12

Угол α между линией ската MN и ее проекцией MN1 называется углом падения плоскости, или углом наибольшего ската плоскости (Рис. 13).

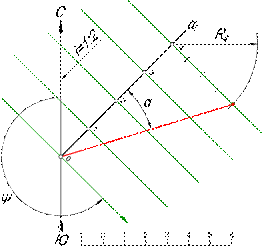
Рис. 13

Масштаб уклона плоскости в проекциях с числовыми отметками - это проекция линии наибольшего ската плоскости и проекции горизонталей плоскости, нанесенных на ней с заданным интервалом.

Угол падения плоскости определяется как угол между натуральной длиной линии наибольшего ската и масштабом уклона плоскости. Для того чтобы найти угол α необходимо построить натуральную длину линии наибольшего ската MN, отложив от точки 4 разность отметок в 4 единицы на перпендикуляре к линии масштаба уклона. Масштаб уклона плоскости определяет положение плоскости в пространстве. Чем меньше уклон плоскости, тем больше интервал между горизонталями плоскости. Чем больше уклон плоскости, тем меньше интервал между горизонталями плоскости.

Направление плоскости и угол простирания плоскости в проекциях с числовыми отметками - эти понятие используют, в тех случаях, когда ориентируют плоскость относительно сторон света. Направление плоскости - это правое направление горизонталей, если смотреть в сторону подъема плоскости. Угол простирания плоскости Ψ - это угол, измеряемый в горизонтальной плоскости против хода часовой стрелки, от северного конца магнитной стрелки до направления линии простирания плоскости (Рис. 14).

Рис. 14

3. 3. 1. Пересечение плоскостей между собой.

Линия пересечения плоскостей в проекциях с числовыми отметками может быть построена, если найдены две точки, принадлежащие обеим плоскостям (Рис. 15).

Рис. 15

Для нахождения точек, принадлежащих этим плоскостям, вводим вспомогательные плоскости. Пересечение их с заданными плоскостями даст линии, в пересечении которых находим точки, принадлежащие исходным плоскостям. В качестве вспомогательных плоскостей используются, как правило, горизонтальные плоскости, проведенные по отметкам горизонталей. В результате чего во вспомогательных плоскостях происходит пересечение горизонталей с одинаковыми отметками, дающее две точки, принадлежащие обеим заданными плоскостям.

Линия пересечения плоскостей в проекциях с числовыми отметками строится, если выполняется проектирование земляного сооружения называемого аппарелью. Аппарель - это наклонный въезд или съезд в выемках или насыпях. Здесь имеют место линии пересечения плоскостей откосов аппарели с плоскостью, принятой за условный уровень и откосов между собой. Откосы аппарели можно рассматривать как касательные плоскости к поверхности прямого кругового конуса, вершина которого скользит по прямой (бровке дороги), а образующая наклонена к плоскости основания под углом, равным углу наклона плоскости откоса.

3. 4. Топографическая поверхность.

Топографическая поверхность - это земная поверхность, также это графическая поверхность закон образования которой неизвестен.

Топографическая поверхность используется при проектировании различных сооружений, дорог, мостов, строительных площадок.

Топографическая поверхность в плане изображается с помощью горизонталей - линий соединяющих точки с одинаковыми отметками. Разность высотных отметок между двумя соседними горизонталями принято брать равными единице. За единицу берут 1 м в том или ином масштабе. Расстояние между горизонталями называется - интервал. Интервал определяет уклон топографической поверхности. Принято считать, что топографическая поверхность в интервалах между горизонталями имеет одинаковый уклон по линии наибольшего ската. План местности, представленный в горизонталях, приведен на рис. 1.

Часть поверхности выраженной в горизонталях в виде замкнутых кривых: - называют вершиной, когда каждая внутренняя горизонталь имеет числовую отметку больше каждой внешней; - называют котловиной, когда каждая внутренняя горизонталь имеет числовую отметку меньше каждой внешней; - называют седловиной, поверхность ограниченную с четырех сторон выпуклыми сторонами горизонталей. При этом противоположные горизонтали образуют одно семейство горизонталей, каждая из которых имеет числовую отметку, меньшую (или большую) числовой отметки каждой горизонтали второго семейства, образованного другими противоположными горизонталями;

- водоразделом (или линией хребта) называют линию наибольшего ската поверхности, проходящей через точки максимальной кривизны горизонталей в случае, когда всякая огибающая горизонталь имеет меньшую числовую отметку, чем огибаемая;

- водосливом (тальвегом) называют линию ската, проходящую через точки максимальной кривизны горизонталей (линия долины), если каждая огибающая горизонталь имеет числовую отметку больше числовой отметки огибаемой горизонтали. Водяные струи всегда стремятся от линии водораздела к линии водослива.

3. 5. Пересечение топографической поверхности с плоскостью

Пересечение плоскости с топографической поверхностью находится отыскиванием точек пересечение их горизонталей, а они пересекутся, только тогда, когда будут иметь одинаковые отметки.

Если при пересечении плоскостей достаточно было найти две точки, принадлежащие линии пересечения, то при пересечении с топографической поверхностью необходимо найти пересечение всех ее горизонталей с горизонталями плоскости. Найденные точки соединяются плавной кривой линий.

Задача на пересечение плоскости с топографической поверхностью используется при определении границ земляных работ, при проектировании земляного сооружения на топографической поверхности (Рис. 16).

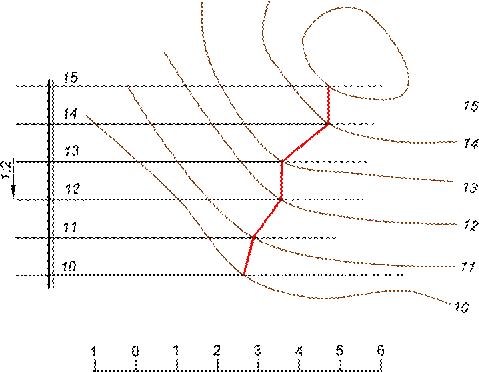
Рис. 16

Профиль - это сечение топографической поверхности вертикальной плоскостью. Горизонтальная проекция такой плоскости проецируется в прямую линию, называемую направлением профилирования.

Профиль для определения рельефа местности и решении специальных задач. Профиль может быть: - продольным, когда направление профилирования совпадает с продольной осью сооружения;

- поперечным, когда направление профилирования поперек сооружения;

- по заданному, когда направление профилирования задается.

Для построения профиля топографической поверхности:

- все точки пересечения плоскости с горизонталями топографической поверхности переносятся на проведенные в стороне или сверху две горизонтальные прямые;

- слева проводим вертикальную прямую и на ней откладываем единицы масштаба, через которые проводим прямые уровня;

- восстановив перпендикуляры из точек пересечения плоскости с горизонталями топографической поверхности, проводим их до линий соответствующего уровня;

- полученные таким образом точки соединяем плавной кривой линией, которая и представляет собой профиль топографической поверхности. Когда рельеф местности выражен слабо, рекомендуется вертикальный масштаб увеличивать в несколько раз, например в 10 раз.

Увеличение вертикального масштаба применяют при решении различных задач на пересечение прямой с поверхностью, например нахождение точки выхода трубопровода на поверхность земли (Рис. 17).

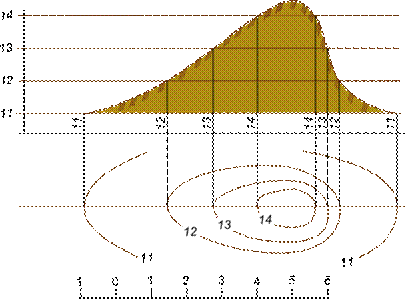
Рис. 17

4. Определение границ выемки и насыпи земляного сооружения

Границы земляных работ для откосов выемки строим по точкам пересечения горизонталей топографической поверхности с горизонталями плоскостей откосов. При этом, находим точку пересечения откосов соседних плоскостей, которая находится на линии пересечения плоскостей откосов (биссектрисе угла).

Границы земляных работ для откосов насыпи строятся по точкам пересечения горизонталей топографической поверхности с горизонталями откосов насыпи. Линии пересечения плоскостей откосов насыпи друг с другом находим также на биссектрисе углов.

Границу земляных работ на конической поверхности строим по точкам пересечения горизонталей топографической поверхности с горизонталями конической поверхности, которые представляют собой дуги окружностей, проведенные через горизонтали масштаба уклонов конической поверхности.

Построение границы земляных работ на аппарелях дороги строим аналогично. При этом горизонтали плоскости откосов дороги касательные к конической поверхности.

В результате получим границы откосов выемки, насыпи и дороги, представленные на рис. 18.

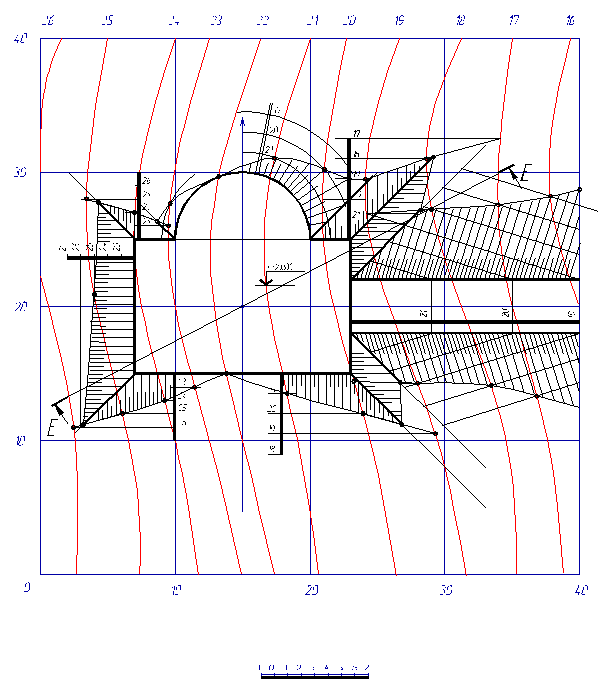
Рис. 18

5. Построение геологического профиля

Построения профиля земляного сооружения по секущей плоскости Е-Е начинаем с горизонтальной линии, на которой откладываем в масштабе все точки пересечения плоскости с горизонталями топографической поверхности.

Проводим вертикальную линию и на ней в том же масштабе (можно с увеличением 5: 1) откладываем числовые отметки земляного сооружения и горизонталей топографической поверхности.

Восстановив перпендикуляры из точек пересечения плоскости с горизонталями топографической поверхности, проводим их до линий соответствующего уровня;

Полученные таким образом точки соединяем плавной кривой линией, которая и представляет собой профиль топографической поверхности.

Профиль земляного сооружения накладываем на профиль топографической поверхности, повторив все построения. В результате получим искомый геологический профиль – сечение земляного сооружения вертикальной плоскостью Е – Е (рис. 19).

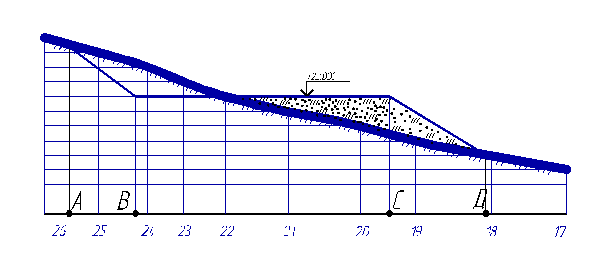
Рис. 19

Заключение

Список использованных источников

1. Начертательная геометрия. Инженерная и компьютерная графика в задачах и примерах: учебное пособие/ П. Н. Учаев С. Г. Емельянов, К. П. Учаева [и др. ]; под общ. ред. проф. П. Н. Учаева. – Старый Оскол: Изд-во ТНТ, 2011. – 288 с. (Гриф УМО АМ).

2. Компьютерные технологии и графика: атлас/ П. Н. Учаев, С. Г. Емельянов, К. П. Учаева, Ю. А. Попов. – Старый Оскол: ТНТ, 2011. – 276 с. (Гриф УМО АМ).

3. Инженерная компьютерная графика. Вводный курс: учебник/ П. Н. Учаев, С. Г. Емельянов, С. А. Чевычелов, Г. Ф. Горшков, К. П. Учаев, В. В. Горетый. – Старый Оскол: ТНТ, 2014. – 216 с. (Гриф УМО АМ).

4. Горетый В. В. Начертательная геометрия. Лекции для заочников: учебное пособие. – Старый Оскол: ООО «ТНТ», 2014. – 87 с.

5. Горетый В. В. Инженерная графика: Учебное пособие. – Старый Оскол: ООО " ТНТ", 2014. – 128 с.

6. Инженерно-геологическая графика: учебник/ Б. М. Ребрик, Н. В. Сироткин, В. Н. Калиничев. – Москва: Изд-во «НТ Прогресс», 2008. – 256 с.

7. Государственные стандарты. Единая система конструкторской документации. ГОСТ 2. 301-68 – ГОСТ 2. 321-84 /электронный ресурс – 10, 5 МБ/. – ИПК Издательство стандартов, 2008. – 161 с.

8. ГОСТ 2. 851 – 75. Горная графическая документация. Общие правила выполнения горных чертежей. – ИПК Издательство стандартов, 2008. – 20 с.

9. Индекс 38845. Журнал. Геометрия и графика. – Naukaru. ru Web site: http: nauka 2. infa-m. ru

10. Индекс 72629. Журнал. САПР и Графика. Web site: http: //www. sapr. ru/archive. aspx.

11. Индекс 72428 Справочник. Инженерный журнал. Web Site: http; //www. tstu. ru/win/tgtu/ips/mag_ing/htm

12.