Пояснения к работе. Рис. 1.1. Схема взаимодействия масс

ВЫЧИСЛЕНИЕ НОРМАЛЬНОГО ЗНАЧЕНИЯ

УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ

Цель работы: вычислить по заданным формулам нормальное значение ускорения силы тяжести в зависимости от широты точки на поверхности Земли в интервале широт от 90° (полюс) до 0° (экватор)

Приборы и оборудование: микрокалькулятор или компьютер.

Пояснения к работе

Гравитационное поле - это поле силы тяжести, то есть поле взаимодействия механических масс в материальной среде (рис. 1. 1).

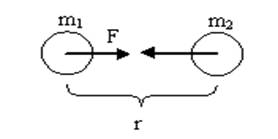
Рис. 1. 1. Схема взаимодействия масс

В основе лежит закон Ньютона:

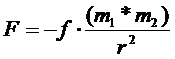(1. 1),

где F - сила притяжения, f - постоянная гравитационного поля, равная

6, 67*10^-8*г^{-1 см 3}сек^-2, m₁ и m₂ - взаимодействующие массы, r - расстояние между m₁ и m₂.

Если m₁ считать точечной массой, а m₂ увеличить до массы Земли, то формула Ньютона примет вид:

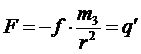(1. 2),

где q^/ - ускорение свободного падения, значение которого с учётом центробежной силы, возникающей от вращения Земли, составляет 9, 81 м/с².

За единицу свободного падения принят 1мГл = 10^-3 см/с².

При проведении гравиразведочных работ измерения выполняются по параметру 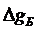- приращение силы тяжести в редукции Буге. Этот параметр является результирующим между аномальным g_аном (измеренным) и нормальным g_нор (теоретическим) значениями силы тяжести. Кроме того, в показания 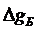вводятся поправки: 1) за свободный воздух 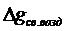, 2) за промежуточный слой пород (толщу пород между точкой наблюдения поверхностью геоида или за поправку Буге 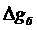), 3) за рельеф 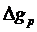(рис. 1. 2).

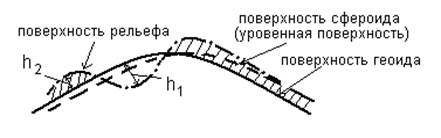
Рис 1. 2. Соотношение уровненных поверхностей геоида и сфероида с поверхностью рельефа. h₁, h₂ - толщины слоев воздуха и пород, залегающих выше поверхности геоида

Параметр g_норм представляет собой ускорение силы тяжести Земли, как сфероида малого сжатия. Последний описывается уровенной поверхностью, близкой к геоиду, который в свою очередь является уровенной поверхностью свободной воды океанов. У поверхности Земли g_норм изменяется от 9, 780 м/с² до 9, 810 м/с². Наблюдаемое увеличение g_норм от экватора к полюсам объясняется, с одной стороны, изменением ускорения центробежной силы, а с другой – уменьшением радиуса Земли примерно на 21 км по оси вращения, то есть сжатием Земли. Имеется (получено) несколько вариантов аналитического расчёта значений нормального гравитационного поля, как для всей поверхности Земли, так и для территорий отдельных государств. В расчётных формулах эмпирические коэффициенты и их количество меняются, что определяется плотностью проведенных наблюдений и точностью измерений.

Показатель g_{св. возд}_. или g_ф (Фая) учитывается в гравиметрических измерениях как поправка за слой воздуха находящийся между точкой наблюдения и поверхностью геоида.

g_ф = 0, 3086 ^. h₁ (1. 3),

где h₁ толщина слоя воздуха.

Параметр g_б вводится в измеренные значения как поправка за промежуточный слой, который еще носит название поправки Буге. Поправка g_б необходима в том случае если измерения производятся в точке, находящейся выше поверхности геоида и, следовательно, проявляется влияние толщи пород заключенных между поверхностью геоида и поверхностью рельефа (см. рис. 1. 2).

g_б = -0, 418 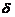h₂ (1. 4),

где 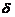- средняя плотность, а h₂ – толщина промежуточного слоя.

Поправка за рельеф 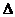g_р учитывается, если этот рельеф очень сложный, например в горной местности.

В конечном виде формула аномальной силы тяжести в редукции Буге включает разность значений наблюденного и теоретического полей и сумму поправок за свободный воздух, промежуточный слой и рельеф:

Dg_б = g_аном - g_норм + g_ф + g_б + g_р (1. 5)

Порядок выполнения работы

Вычислить нормальное значение ускорения силы тяжести на поверхности Земли в интервале широт от 90° (полюс) до 0° (экватор) по формуле Гельмерта 1884 г. и одной из формул, приведенных в задании. Шаг изменения широты j принять 10°, а величину долготы l равной 60°. По результатам расчётов построить сводный график изменения нормального значения ускорения силы тяжести в зависимости от широты.

Пример выполнения и оформления результатов по 1-ой части задания приведен на рисунке 1. 3. Для этого в программе Excel составляется таблица исходных данных широты и долготы точек на поверхности Земли. Соответствующие формулы (см. варианты задания) вводятся в определенные ячейки таблицы и автораспространяются протаскиванием при нажатой левой клавиши мыши на другие ячейки.

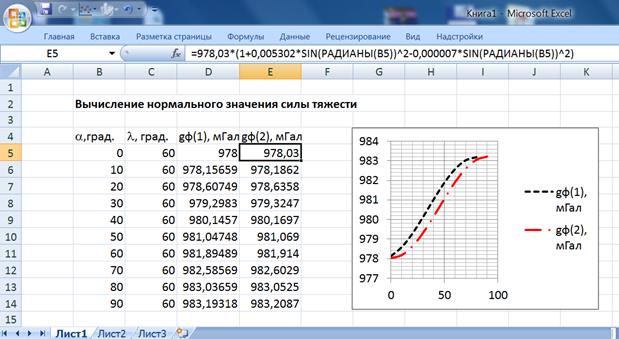
Рис. 1. 3. Пример расчёта в программе Excel нормального значения ускорения

силы тяжести в зависимости от широты

Варианты задания (расчётные формулы: 1-15) по 1-ой части:

1. Гельмерт, 1884 г.

g_ф = 978, 00(l + 0, 005310 sin²j);

2. Гельмерт, 1901-1909 гг.

g_ф = 978, 030 (l + 0, 005302 sin²j - 0, 000007·sin²j);

3. Гельмерт, 1915 г.

g_ф = 978, 052 [l + 0, 005285 sin²j - 0, 000007 sin²j +

+ 0, 000018 cos²a·cos2(l+17°)];

4. Боуи, 1917 г.

g_ф = 978, 039 (l + 0, 005294 sin²j - 0, 000007 sin²j);

5. Гейсканен, 1924 г.

g_ф = 978, 052 [l + 0, 005285 sin²j- 0, 000007 sin²j +

+ 0, 000027 cos² j cos2(l+18°)];

6. Гейсканен, 1928 г.

g_ф = 978, 049 [l + 0, 005293 sin²j - 0, 000007 sin²2j+

+ 0, 000019 cos²j сos2(l+0°)];

7. Гейсканен, 1928 г.

g_ф = 978, 049 (l + 0, 005289 sin²j - 0, 000007 sin²2j);

8. Кассинис, 1930 г.

g_ф = 978, 049 (l + 0, 0052884 sin²j- 0, 0000059 sin²2j);

9. Гейсканен, 1938 г.

g_ф = 978, 0524 [l + 0, 0052970 sin²j-0, 0000059 sin²2j +

+ 0, 0000276 cos²j cos2(l+25°)];

10. Жонглович, 1952 г.

g_ф = 978, 0573 (l + 0, 0052837 sin²j-0, 0000059 sin²2j);

11. Жонглович, 1952 г.

g_ф = 978, 0573 [l + 0, 005268 sin²j- 0, 0000059 sin²2j +

+ 0, 0000155 cos²j cos2(l+6°)];

12. Гейсканен, 1957 г.

g_ф = 978, 0497 (l + 0, 0032902sin²j> - 0, 0000059sin²2j);

13. Гейсканен, 1957 г.

g_ф = 978, 0516 [l + 0, 0052910 sin²j - 0, 0000059 sin²2j +

+ 0, 0000106 cos²j cos2(l+6°)];

14. Грушинский, 1960 г.

g_ф = 978, 0531 (l + 0, 0052883 sin²j - 0, 0000059 sin²2j);

15. Международная формула, 1967 г.

g_ф = 978, 01318(l + 0, 0053024 sin²j - 0, 0000059 sin²2j).

Контрольные вопросы

1. Раскройте сущность гравитационного поля Земли?

2. Какие поправки вводятся в формулу аномальной силы тяжести в редукции Буге?

3. Почему существует много формул нормального ускорения силы тяжести?

Сущность методики расчёта относительного изменения