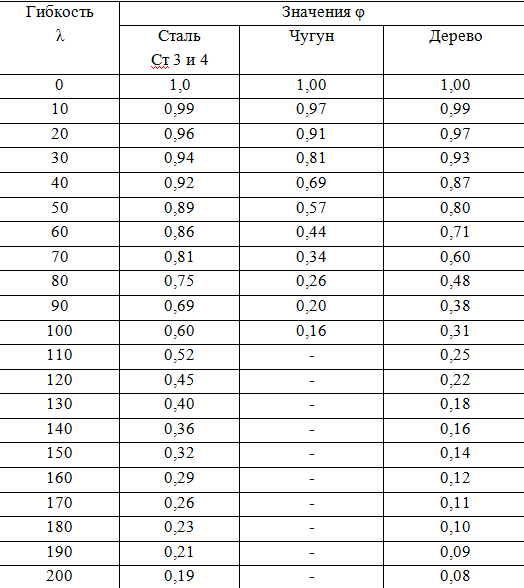
Значения коэффициента φ в зависимости от гибкости λ для материалов

Задачи на устойчивость сжатых стержней

Условием устойчивости сжатого стержня является неравенство:

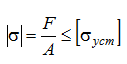
Здесь допускаемое напряжение по устойчивости [σ _уст] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих факторов:

1) от длины стержня, от размеров и даже от формы поперечных сечений,

2) от способа закрепления концов стержня,

3) от материала стержня.

Как и всякая допускаемая величина, [σ _уст] определяется отношением опасного для сжатого стержня напряжения к коэффициенту запаса. Для сжатого стержня опасным является так называемое критическое напряжение σ _кр, при котором стержень теряет устойчивость первоначальной формы равновесия.

Поэтому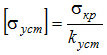

Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷ 2, то k_уст=2÷ 5.

Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности: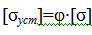

В этом случае ,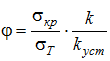

где σ _т – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатие σ _вс ).

Коэффициент φ < 1 и потому называется коэффициентом снижения основного допускаемого напряжения, то есть [σ ] по прочности, или иначе коэффициентом продольного изгиба.

С учетом сказанного условие устойчивости сжатого стержня принимает вид:

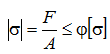
Численные значения коэффициента φ выбираются из таблиц в зависимости от материала и величины гибкости стержня 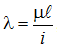, где:

μ – коэффициент приведенной длины (зависит от способов закрепления концов стержня), Значения μ приведены под соответствующей схемой закрепления стержней

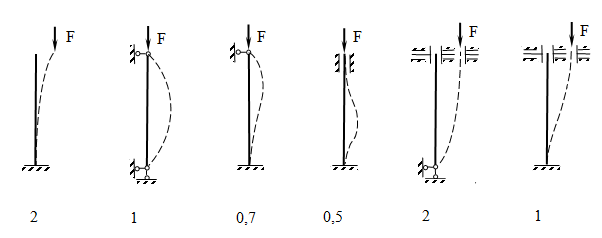
ℓ — геометрическая длина стержня,

i – радиус инерции поперечного сечения 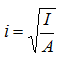относительно той из главных центральных осей сечения, вокруг которой будет происходить поворот поперечных сечений после достижения нагрузкой критического значения.

Коэффициент φ изменяется в диапазоне 0≤ φ ≤ 1, зависит, как уже говорилось, как от физико-механических свойств материала, так и от гибкости λ. Зависимости между φ и λ для различных материалов представляются обычно в табличной форме с шагом ∆ λ =10.

При вычислении значений φ для стержней, имеющих значения гибкости не кратные числу 10, применяется правило линейной интерполяции.

Значения коэффициента φ в зависимости от гибкости λ для материалов

На основании условия устойчивости решаются три вида задач:

Проверка устойчивости.
Подбор сечения.
Определение допускаемой нагрузки (или безопасной нагрузки, или грузоподъемности стержня: [F]=φ [σ ]А.

Наиболее сложным оказывается решение задачи о подборе сечения, поскольку необходимая величина площади сечения входит и в левую, и в правую часть условия устойчивости:

Только в правой части этого неравенства площадь сечения находится в неявном виде: она входит в формулу радиуса инерции 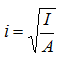, который в свою очередь включен в формулу гибкости 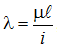, от которой зависит значение коэффициента продольного изгиба φ. Поэтому здесь приходится использовать метод проб и ошибок, облеченный в форму способа последовательных приближений:

1 попытка: задаемся φ ₁ из средней зоны таблицы, находим 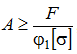, определяем размеры сечения, вычисляем 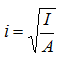, затем гибкость 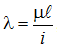, по таблице определяем 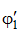и сравниваем со значением φ 1. Если 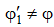, то:

2 попытка: принимаем 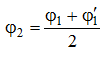, находим 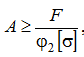, определяем размеры сечения, вычисляем 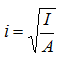, затем гибкость 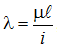, по таблице определяем 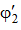, и если 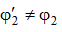, то:

3 попытка: принимаем 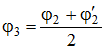, находим 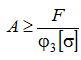, определяем размеры сечения, вычисляем 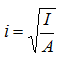, затем гибкость 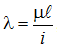, по таблице определяем 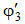, и т. д.

Процесс приближений продолжается до тех пор, пока разница не окажется менее 5%.