
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение. Фигуру, ограниченную графиком функции f и прямыми у=0, х=а и х=b, называют криволинейной трапецией.
Площадь криволинейной трапеции
Рассмотрим функцию 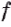 , которая непрерывна на отрезке
, которая непрерывна на отрезке 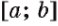 и принимает на этом промежутке неотрицательные значения.
и принимает на этом промежутке неотрицательные значения.
Определение. Фигуру, ограниченную графиком функции f и прямыми у=0, х=а и х=b, называют криволинейной трапецией.
На рисунке приведены примеры криволинейных трапеций.
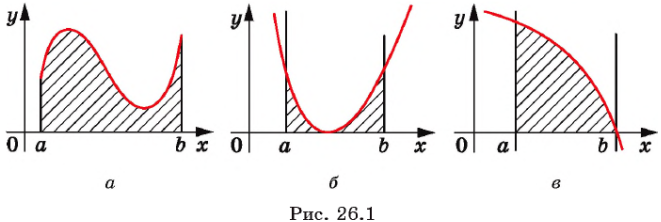
Рассмотрим теорему, которая позволяет вычислять площади криволинейных трапеций.
Теорема.
Площадь S криволинейной трапеции, ограниченной графиком функции и прямыми у = f(x), у = 0, х = а, х = b, aбольше b, можно вычислить по формуле
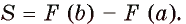
где F — любая первообразная функции f на отрезке [a; b]
Примеры с решением
Пример 1.
Найдите площадь 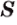 фигуры, ограниченной графиком функции
фигуры, ограниченной графиком функции 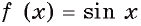 и прямыми
и прямыми 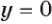 ,
, 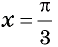 и
и 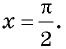
Решение:
На рисунке 26. 5 изображена криволинейная трапеция, площадь которой требуется найти.
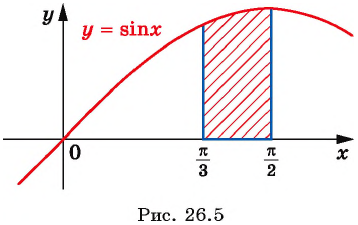
Одной из первообразных функции 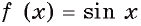 на отрезке
на отрезке 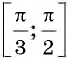 является функция
является функция 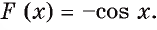 Тогда
Тогда
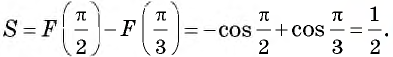
Пример 2.
Найдите площадь 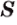 фигуры, ограниченной графиком функции
фигуры, ограниченной графиком функции 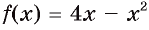 и прямой
и прямой 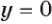 .
.
Решение:
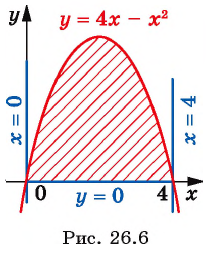
График функции 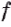 пересекает прямую
пересекает прямую 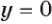 в точках
в точках 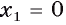 и
и 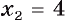 (рис. 26. 6). Тогда фигура, площадь которой требуется найти, является криволинейной трапецией, ограниченной графиком функции
(рис. 26. 6). Тогда фигура, площадь которой требуется найти, является криволинейной трапецией, ограниченной графиком функции 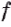 и прямыми
и прямыми 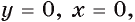
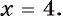
Одной из первообразных функции 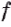 на отрезке
на отрезке 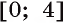 является функция
является функция 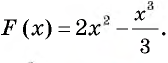 Тогда
Тогда 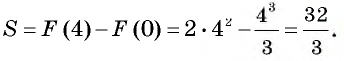
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|