
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Изменения в профильном ЕГЭ по математике
Изменения в профильном ЕГЭ по математике
Карачинский Е. Я.
С 2022 года в профильный ЕГЭ по математике внесены следующие изменения:
1) Первые три задачи первой части исключены из экзамена. Вместо них будут добавлены две: одна на функции и их графики, другая-на элементы статистики и теории вероятностей. Таким образом, задания с кратким ответом будут насчитывать 11 заданий.
2) Во второй части так называемая «экономическая» задача будет оцениваться из 2 баллов, а задача по стереометрии из 3 баллов. Здесь остается 7 заданий.
3) Будет изменена шкала перевода первичных баллов (максимальный балл теперь стал 31) в тестовые.
Тем самым учтены некоторые мои предложения, опубликованные в предыдущей статье, смысл которых был в том, что при существовании базового ЕГЭ профильный экзамен не должен содержать совсем уж примитивных заданий, а «цена» задач по геометрии во 2 части должна быть повышена.
Настала пора задуматься о стратегии дальнейшего развития единого государственного экзамена. Мне представляется, что тестовая часть выглядит теперь вполне разумно. Пожалуй, тематику второй задачи о вероятности я дополнил бы комбинаторикой. Прототипы всех заданий и дальше следует размещать в открытом банке задач ЕГЭ.
Что же касается заданий с развернутым ответом, то я по-прежнему считаю, что вместо финансовой задачи должна появиться задача на применение производной, причем, не исключено. что с практическим содержанием. Но главное: нужно двигаться в сторону постепенной отмены «закрепления» за номером задания его типа! Следует оставить только спецификацию заданий для второй части.
Также очень важным мне представляется менять тематику заданий внутри конкретной задачи.
Например, это может выглядеть так:
Во второй части планируется 7 заданий, соответствующих следующим темам:
1. Числа: натуральные, целые, рациональные, действительные, комплексные числа, их геометрическая интерпретация и свойства. Делимость целых чисел. Числовые средние. Последовательности и прогрессии.
2. Уравнения: рациональные, иррациональные, показательные, логарифмические, тригонометрические. Различные способы их решения. Функциональный подход к решению уравнений. Системы уравнений с двумя переменными.
3. Неравенства: рациональные, иррациональные, показательные, логарифмические. Метод интервалов, в том числе, обобщенный. Функциональный подход к решению неравенств. Системы неравенств с одной переменной.
4. Применение производной: уравнение касательной, критерии монотонности, необходимые и достаточные условия экстремумов функций, построение графиков с помощью производной, нахождение наибольшего и наименьшего значений функции на отрезке, задачи на оптимизацию.
5. Планиметрия
6. Стереометрия
7. Задача с параметром: аналитический, графо-аналитический, графический способы решения
Каждая из задач может оказаться на любой позиции и оцениваться от 2 до 4 баллов в зависимости от сложности в данном варианте (так, чтобы, как и прежде, было 3 задачи по 2 балла, 2 задачи по 3 балла и 2 задачи по 4 балла).
Ниже приводятся по 3 примерные задачи каждого вида (на 2, на 3 и на 4 балла):
1. 1) (2 балла) Найдите все такие натуральные a такие, что 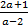 - целое число.
- целое число.
2) (3 балла) Из всех чисел z, удовлетворяющих условию 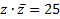 , найдите такие, что
, найдите такие, что
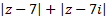 принимает наименьшее значение.
принимает наименьшее значение.
3) (4 балла) На доске написано более 40, но не более 48 целых чисел. Среднее арифметическое этих чисел равно -3. Среднее арифметическое всех положительных из них чисел равно 4, а среднее арифметическое отрицательных из них равно -8.
а) Сколько чисел написано на доске?
б) Каких чисел больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
2. 1) (2 балла) а) 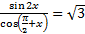 ; б) Укажите корни этого уравнения, принадлежащие отрезку
; б) Укажите корни этого уравнения, принадлежащие отрезку 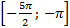
2) (3 балла) 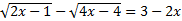
3) (4 балла) 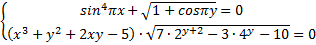
3. 1) (2балла) 2 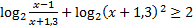
2) (3 балла) 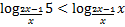
3) (4 балла) 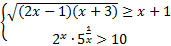
4. 1) (2балла) Среди всех прямоугольников с диагональю 18 найти прямоугольник с
наибольшей площадью.
2) (3 балла) В арифметической прогрессии шестой член равен 3, разность прогрессии
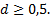 Прикаком значении d произведение первого, четвертого и пятого членов
Прикаком значении d произведение первого, четвертого и пятого членов
будет наибольшим?
3) (4 балла) Определите координаты точки графика функции 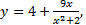 сумма
сумма
расстояний от которых до осей координат наименьшая.
5. 1) (2 балла) Боковая сторона ABтрапеции ABCDравна l, а расстояние от середины CDдо
прямой ABравно m. Найдите площадь трапеции.
2) (3балла) Точка O-центр окружности, описанной около остроугольного треугольника
ABC, а BH-высота этого треугольника.
а) Докажите, что углы ABHи CBOравны
б) Найдите BH, если AB=8, BC=9, BH=BO
3) (4 балла) Дан выпуклый четырехугольник ABCDсо сторонами AB=3, BC=CD=5, AD=8 и
диагональю AC=7.
а) Докажите, что около него можно описать окружность
б) Найдите диагональ BD.
6. 1) (2 балла) Две параллельные плоскости, находящиеся на расстоянии 12 друг от друга,
пересекают шар. Получившиеся сечения равны, и площадь каждого из них 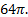
Найдите площадь поверхности шара.
2) (3 балла) В основании правильной четырехугольной пирамиды MABCDлежит
квадрат ABCD. Противоположные боковые грани пирамиды попарно
перпендикулярны. Через середины ребер MAи MBпроведена плоскость 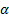 ,
,
параллельная ребру MC.
а) Докажите, что плоскость 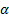 параллельна ребру MD.
параллельна ребру MD.
б) Найдите угол между плоскостью 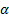 и прямой AC.
и прямой AC.
3) (4 балла) Все ребра правильной треугольной призмы 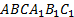 имеют длину 6.
имеют длину 6.
Точки Mи N- середины ребер 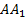 и
и 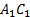 соответственно.
соответственно.
а) Докажите, что прямые BMи MNперпендикулярны.
б) Найдите угол между плоскостями BMNи 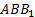
7. 1) (2 балла) При каком наибольшем значении параметра aфункция
 возрастает на
возрастает на 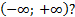
2) (3 балла) Выясните, при каких значениях параметра aуравнение имеет четное
число решений на отрезке 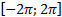 :
: 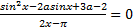 ?
?
3) (4 балла) Найдите все значения параметра a, при которых уравнение
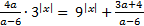 имеет ровно два различных корня.
имеет ровно два различных корня.
Приведенная мною в 1 части сборника демонстрационная версия заданий второй части может выглядеть так (она собрана из опубликованных выше задач). Привожу ее теперь с решениями и разработанными мною критериями):
12. Найдите все такие натуральные a такие, что 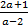 - целое число.
- целое число.
Решение: 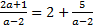 , откуда
, откуда 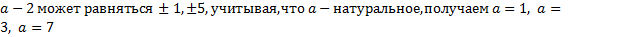
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного на одно из значений a | |
| Не удовлетворяет ни одному из критериев |
13. а) Решите уравнение: 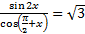 ; б) Укажите корни этого уравнения, принадлежащие отрезку
; б) Укажите корни этого уравнения, принадлежащие отрезку 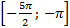
Решение:  ;
; 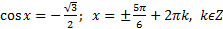
б) На 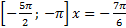 (при
(при 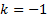 в
в 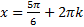 , остальные целые k
, остальные целые k
не удовлетворяют условию)
| Обоснованно получен верный ответ в пунктах а и б | |
| Обоснованно получен верный ответ в пункте а Или Обоснованно получен верный ответ в пункте б из верного простейшего тригонометрического уравнения, полученного в пункте а Или Обоснованно получен верный ответ в пунктах а и б, но содержится ошибка в нахождении ОДЗ | |
| Не удовлетворяет ни одному из критериев |
14. Решите неравенство: 2 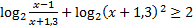
Решение: ОДЗ неравенства: 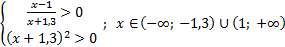 ;
;
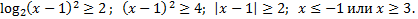 С учетом ОДЗ получаем
С учетом ОДЗ получаем
ответ: 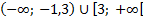
| Обоснованно получен верный ответ | |
| Получен ответ, отличающийся от верного исключением точки 3 Или Получен неверный ответ из-за одной арифметической ошибки или описки, но имеется верная последовательность всех шагов решения | |
| Не удовлетворяет ни одному из критериев |
15. В арифметической прогрессии шестой член равен 3, разность прогрессии 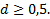 При
При
каком значении d произведение первого, четвертого и пятого членов будет наибольшим?
Решение: 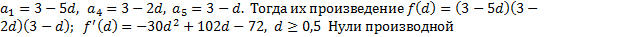
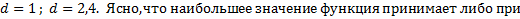
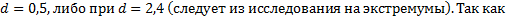
 , то наибольшее произведение будет при
, то наибольшее произведение будет при 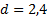
| Обоснованно получен верный ответ | |
| Получен верный ответ, но не обосновано, почему наибольшее значение принимается при d=2, 4 Или Обоснованно получен ответ, неверный из-за одной арифметической ошибки или описки | |
| Верно составлена функция, которую необходимо исследовать, дальнейшее решение неверно или не завершено | |
| Не удовлетворяет ни одному из критериев |
16. Точка O-центр окружности, описанной около остроугольного треугольника
ABC, а BH-высота этого треугольника.
а) Докажите, что углы ABH и CBO равны
б) Найдите BH, если AB=8, BC=9, BH=BO
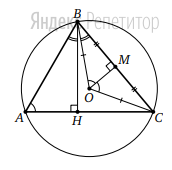
Решение: а) Обозначим угол BAC через 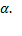 Тогда
Тогда 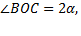 поскольку является
поскольку является
центральным углом, опирающимся на ту же дугу окружности, что и угол BAC.
В равнобедренном треугольнике BOC получаем 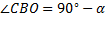 , в прямоугольном
, в прямоугольном
треугольнике BAH получаем 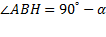 . Таким образом,
. Таким образом, 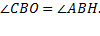
б) Пусть M — середина отрезка BC. Прямоугольные треугольники BAH и BOM подобны,
поскольку 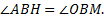 Значит,
Значит, 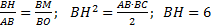
| Обоснованнои верно выполнены пункты а и б | |
| Обоснованно получен верный ответ в пункте б без использования результата пункта а Или Верно выполнен пункт а и обоснованно получен ответ в пункте б, неверный из-за арифметической ошибки или описки | |
| Верно выполнен пункт а Или Обоснованно получен верный ответ в пункте б с использованием результата пункта а, при этом пункт а не выполнен Или Обоснованно получен ответ в пункте б, неверный из-за арифметической ошибки или описки | |
| Не удовлетворяет ни одному из критериев |
17. Все ребра правильной треугольной призмы 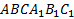 имеют длину 6. Точки M и N-
имеют длину 6. Точки M и N-
середины ребер 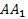 и
и 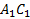 соответственно.
соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и 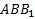 .
.
Решение: а) Проведем в основании призмы высоту BH, причем точка H-середина AC.
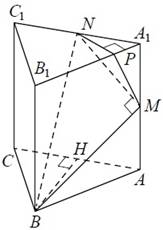
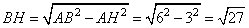 .
.
Вычислим длину отрезка BN из прямоугольного треугольника BNH
также по теореме Пифагора:
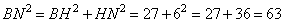 .
.
Чтобы доказать перпендикулярность отрезков BM и MN нужно показать,
что их сумма квадратов будет равна 63:
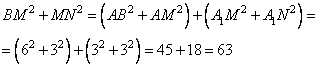
следовательно, по теореме, обратной теореме Пифагора, треугольник
BMN является прямоугольным с прямым углом M.
б) Сначала проведем перпендикуляр NP к прямой 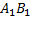 . Тогда получим,
. Тогда получим,
что 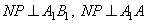 , и, следовательно,
, и, следовательно, 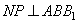 . Отсюда следует, что прямая
. Отсюда следует, что прямая
NP – это проекция MN на плоскость AB 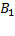 .
.
В предыдущем пункте было показано, что 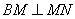 и по теореме о трех
и по теореме о трех
перпендикулярах имеем 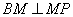 . Следовательно, угол NMP – линейный угол искомого
. Следовательно, угол NMP – линейный угол искомого
угла между плоскостями BMN и AB 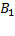 . Вычислим этот угол.
. Вычислим этот угол.
Найдем длину отрезка NP. Так как точка N – середина отрезка 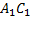 , то длина NP будет в
, то длина NP будет в
два раза меньше высоты треугольника 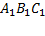 . Так как этот треугольник равносторонний,
. Так как этот треугольник равносторонний,
то его исходная высота равна 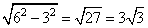 , следовательно,
, следовательно, 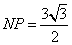 . Тогда
. Тогда
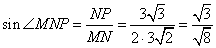
и
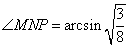
| Обоснованно и верно выполнены пункты а и б | |
| Верно выполнен пункт а и обоснованно получен ответ в пункте б, неверный из-за арифметической ошибки или описки | |
| Верно выполнен пункт а Или Обоснованно получен верный ответ в пункте б | |
| Обоснованно получен ответ в пункте б, неверный из-за арифметической ошибки или описки | |
| Не удовлетворяет ни одному из критериев |
18. Найдите все значения параметра a, при которых уравнение 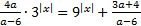 имеет
имеет
ровно два различных корня.
Решение: 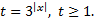 Для того чтобы исходное уравнение имело два различных корня,
Для того чтобы исходное уравнение имело два различных корня,
квадратное уравнение 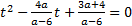 должно либо иметь единственный корень,
должно либо иметь единственный корень,
больший 1, либо два различных корня, лежащих по разные стороны от числа 1.
1) 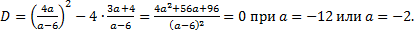 Проверка показывает, что только при
Проверка показывает, что только при 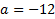 получаем корень
получаем корень 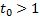
2) Корни квадратного уравнения лежат по разные стороны от числа 1 тогда и только тогда, когда 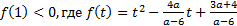 ;
; 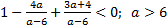
Ответ: 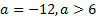
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного включением числа 6 или числа -2 Или Обоснованно получен ответ, неверный из-за одной арифметической ошибки или описки | |
Обоснованно получен ответ, отличающийся от верного включением чисел 6 и -2
Или
Обоснованно получен ответ 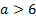 или или 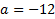
| |
| Задача верно сведена к исследованию квадратного уравнения, дальнейшее решение неверно или не завершено | |
| Не удовлетворяет ни одному из критериев |
Думаю, что такие изменения будут способствовать тому, что учителя смогут вместо
натаскивания на задачи ЕГЭ заниматься изучением программы по математике углубленного
уровня. А это неизбежно, хотя и не сразу, приведет к повышению качества математического
образования в стране.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|