
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Геометрия 8 класс. Тема: МНОГОУГОЛЬНИКИ
Геометрия 8 класс
Тема: МНОГОУГОЛЬНИКИ
Мы рассмотрим понятия многоугольника и выпуклого многоугольника, а также четырехугольника, как частный вид многоугольника; научимся объяснять, какая фигура называется многоугольником, и называть его элементы, рассмотрим формулу нахождения суммы углов выпуклого многоугольника.
Многоугольник - фигура, составленная из отрезков так, что смежные отрезки (имеющие общую точку) лежат на одной прямой, а не смежные отрезки не имеют общих точек.
Каждый многоугольник делит плоскость на две области: внутреннюю и внешнюю.
Многоугольники бывают выпуклые и невыпуклые.
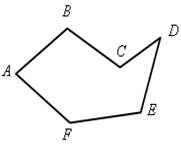
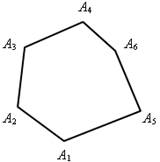
А1А2А3А4А5А6 – выпуклый шестиугольник; ABCDEF – невыпуклый шестиугольник
Рассмотрим элементы выпуклого многоугольника А1А2А3А4А5А6:
1) А1, А2 , А3 , А4 , А5 , А6 - вершины,
2) 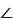 A1,
A1, 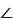 А2,
А2, 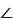 А3,
А3, 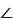 А4,
А4, 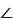 А5,
А5, 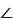 А6 – углы,
А6 – углы,
3) А1А2 , А2А3 , А3А4 , А4А5 , А5А6, А6А1 – стороны,
4) А1А3, А1А4 , А1А5, А1А6, … - диагонали (отрезки, соединяющие противолежащие вершины).
P = А1А2 + А2А3 + А3А4 + А4А5 + А5А6 + А6А1 – периметр.
(n – 2) · 180º - сумма внутренних углов выпуклого многоугольника (n-угольника), где n – количество его сторон.
Частный вид выпуклого многоугольника – четырёхугольник.
Четырёхугольник- многоугольник с четырьмя вершинами.
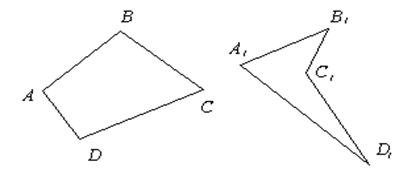
А1В1С1D1 – невыпуклый четырёхугольник,
АВСD – выпуклый четырёхугольник, где
1) А, В, С, D – вершины, из них А и С, В и D – противолежащие,
А и В, А и D, В и С, С и D – соседние.
2)  А,
А,  В,
В,  С,
С, 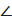 D – углы, из них
D – углы, из них 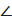 А и
А и 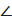 С,
С, 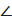 В и
В и 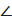 D – противолежащие,
D – противолежащие,
 А и
А и 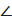 В,
В, 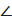 А и
А и 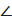 D,
D, 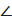 В и
В и 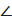 С,
С, 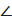 С и
С и 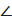 D – соседние.
D – соседние.
3) АВ, ВС, СD, АD – стороны, из них
АВ и АD, ВА и ВС, СВ и СD, DС и DА – соседние (с общей вершиной),
АВ и DС, ВС и АD – противолежащие (не имеют общей вершины),
4) АС и ВD – диагонали.
P = АВ+ВС+СD+АD – периметр.
По формуле (n – 2) · 180º найдём сумму углов выпуклого четырёхугольника:
n = 4, значит (4-2) · 180º = 2 · 180º = 3600.
Домашнее задание:
прочитать п. 40-42, выполнить в тетради:
№ 1. Укажите:
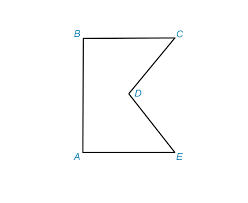
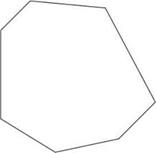
1) Какие из указанных фигур являются многоугольниками?
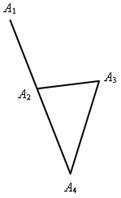 2) Какие из многоугольников являются выпуклыми?
2) Какие из многоугольников являются выпуклыми?
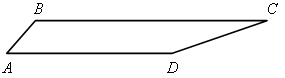
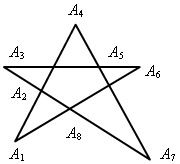 а) б) в)
а) б) в)
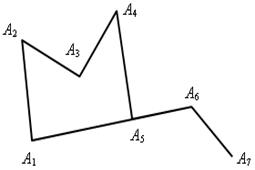
г) д) е)
№ 2. Начертите выпуклый семиугольник, восьмиугольник, девятиугольник и проведите все диагонали из какой-нибудь одной его вершины. Сколько получилось треугольников в каждом случае?
№ 3. Найдите сумму углов выпуклого семнадцатиугольника.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|