Движение с постоянным ускорением

Движение с постоянным ускорением

Выясним зависимость скорости точки от времени при её движении с постоянным ускорением. Для этого воспользуемся формулой

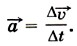
Пусть ₀ — скорость точки в начальный момент времени t₀, а — её скорость в некоторый момент времени t, тогда за промежуток времени Δ t = t - t₀ изменение скорости Δ = - ₀, и формула для ускорения примет вид

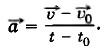
Если начальный момент времени t₀ принять равным нулю, то получим

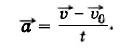
Отсюда получим формулу для определения скорости точки в любой момент времени при её движении с постоянным ускорением:

= ₀ + 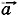t. (1)

Векторному уравнению (1) соответствуют в случае движения на плоскости два скалярных уравнения для проекций скорости на координатные оси X и Y:

_x = _0x +a_xt,
_y = _0y + a_yt. (1. 1)

Как видим, при движении с постоянным ускорением скорость со временем меняется по линейному закону.

Итак, для определения скорости в произвольный момент времени надо знать начальную скорость ₀ и ускорение t Начальную скорость нужно измерить.

Ускорение же, наоборот, не зависит от того, что происходило с телом в предыдущие моменты, а зависит лишь от действия на него других тел в данный момент времени.

Зависимость проекции скорости от времени можно изобразить наглядно с помощью графика.

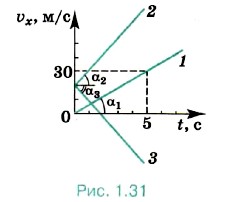
Если начальная скорость равна нулю, то график зависимости проекции скорости на ось X от времени имеет вид прямой, выходящей из начала координат. Такая зависимость скорости от времени наблюдается при падении тела, покоившегося в начальный момент времени, с некоторой высоты или при движении автомобиля, трогающегося с места. На рисунке 1. 31 представлен этот график в виде прямой 1 для случая а_х > 0. По этому графику можно найти проекцию ускорения на ось X:

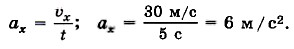
Чем больше а_х, тем больший угол α с осью времени составляет график проекции скорости, так как за тот же промежуток времени скорость изменяется больше.