
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
На этом уроке мы повторим важное свойство числовой окружности и поместим единичную числовую окружность в координатную плоскость по определенным правилам. Вспомним уравнение единичной числовой окружности и с его помощью решим несколько задач на нахождение
На этом уроке мы повторим важное свойство числовой окружности и поместим единичную числовую окружность в координатную плоскость по определенным правилам. Вспомним уравнение единичной числовой окружности и с его помощью решим несколько задач на нахождение координат точки на единичной числовой окружности. В конце урока составим таблицу координат для точек кратных π /6 и π /4.
Тема урока, повторение
Ранее мы изучили числовую окружность и выяснили её свойства (рис. 1).
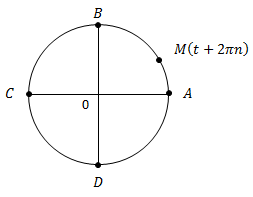
Рис. 1
Каждому действительному числу 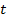 соответствует единственная точка
соответствует единственная точка 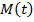 на окружности.
на окружности.

Каждой точке 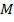 на числовой окружности соответствует не только число
на числовой окружности соответствует не только число 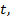 но и все числа вида
но и все числа вида 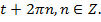
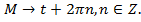
Числовая окружность в координатной плоскости
Поместим окружность в координатную плоскость. По прежнему, каждому числу соответствует точка на окружности. Теперь этой точке на окружности соответствуют две координаты, как и любой точке координатной плоскости.
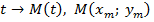 (рис. 2).
(рис. 2).
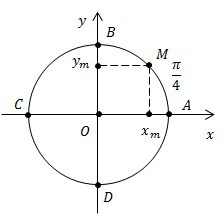
Рис. 2
Наша задача – по данному числу 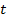 найти не только точку, но и её координаты, и наоборот, по координатам найти одно или несколько соответствующих чисел.
найти не только точку, но и её координаты, и наоборот, по координатам найти одно или несколько соответствующих чисел.
Нахождение прямоугольных координат точек, криволинейные координаты которых кратны 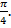
Пример 1. Дана точка  – середина дуги
– середина дуги 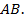 Точке
Точке 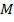 соответствуют числа вида
соответствуют числа вида 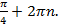
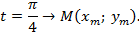
Найти координаты точки 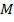 (рис. 3).
(рис. 3).
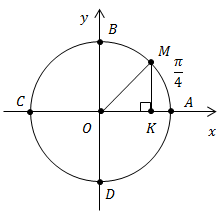
Рис. 3
Решение:
Координаты можно найти двумя разными способами, рассмотрим их по очереди.
1. Точка 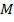 лежит на окружности, R=1, значит, она удовлетворяет уравнению окружности
лежит на окружности, R=1, значит, она удовлетворяет уравнению окружности 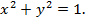
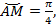 по условию. Мы помним, что величина центрального угла численно равна длине дуги в радианах, значит, угол
по условию. Мы помним, что величина центрального угла численно равна длине дуги в радианах, значит, угол 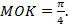 Это значит также, что прямая
Это значит также, что прямая 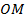 делит первую четверть ровно пополам, значит, это прямая
делит первую четверть ровно пополам, значит, это прямая 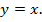
Точка 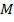 лежит на прямой
лежит на прямой 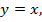 поэтому удовлетворяет уравнению этой прямой.
поэтому удовлетворяет уравнению этой прямой.
Составим систему из двух уравнений.
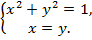
Решив систему, получим искомые координаты.
2. Рассмотрим  прямоугольный (рис. 4).
прямоугольный (рис. 4).
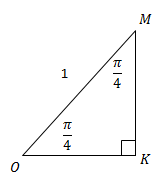
Рис. 4
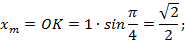

Итак, мы задали число  нашли точку
нашли точку  и её координаты. Определим также координаты симметричных ей точек (рис. 5).
и её координаты. Определим также координаты симметричных ей точек (рис. 5).
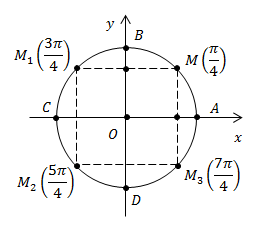
Рис. 5
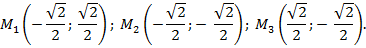
Нахождение прямоугольных координат точек, криволинейные координаты которых кратны 
Следующая задача – таким же образом определить координаты точек, кратных 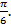
Окружность радиуса R=1 помещена в координатную плоскость, 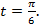 Найти точку на окружности и её координаты (рис. 6).
Найти точку на окружности и её координаты (рис. 6).
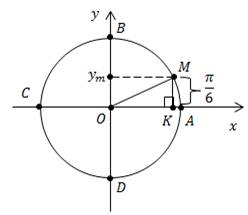
Рис. 6
Решение:
Рассмотрим 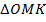 – прямоугольный.
– прямоугольный.
 т. е. угол
т. е. угол 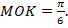
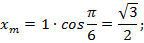
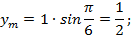

Найдем координаты симметричных точек (рис. 7).
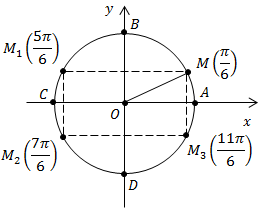
Рис. 7
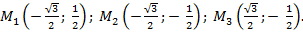
Мы задали число 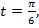 нашли точку на окружности, эта точка единственная, и нашли её координаты.
нашли точку на окружности, эта точка единственная, и нашли её координаты.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|