Тема: Призма. Прямая и наклонная призма. Площадь поверхности, объем призмы.

Тема: Призма. Прямая и наклонная призма. Площадь поверхности, объем призмы.

О: Призмой называется многогранник, две грани которого 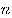-угольники, а остальные 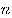граней — параллелограммы.

Многоугольники называют основаниями призмы, параллелограммы - боковыми гранями призмы. Стороны всех граней называют ребрами призмы, концы ребер - вершинами призмы. Стороны боковых граней называют боковыми ребрами.

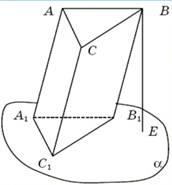
Перпендикуляр, проведенный из какой-либо точки одного основания к плоскости другого основания, называется высотой призмы. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы. Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой.

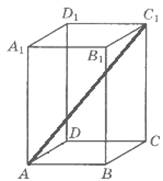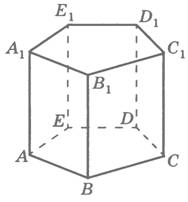
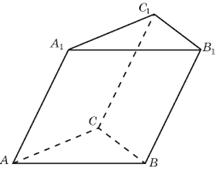В противном случае призма называется наклонной.

У прямой призмы боковые грани – прямоугольники.

Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если она прямая, и ее основания — правильные многоугольники.

Свойства призмы:

1) Основания призмы равны и

лежат в параллельных плоскостях.

2) боковые ребра параллельны и равны;

3) боковые грани - параллелограммы;

Площадь поверхности и объём призмы

Площадь боковой поверхности прямой призмы (S_бок) равна произведению периметра основания (Р_осн) на высоту призмы (Н), т. е. на длину бокового ребра.

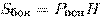
Площадь полной поверхности призмы (S_пр) равна сумме площади боковой поверхности (S_бок) и удвоенной площади основания (S_осн).

S_пр = S_бок + 2S_осн

Объем призмы (V) равен произведению площади основания на высоту

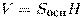
III. Решение задач:

Задача 1. В правильной n-угольной призме сторона основания равна а и высота равна h. Вычислите площади боковой и полной поверхности призмы, если: n = 4, а=12дм, h=8дм.

Дано: n = 4, а = 12 дм, h = 8 дм Найти: S_боки S_пол–?

Решение:

S_бок = 4аh                                                            S_пол = 2S_осн + S_бок
S_бок = 4· 8 · 12 = 384 (дм²)                                S_осн = а² = 12² = 144 (дм²)
                                                                           S_пол= 2· 144 + 384 = 672 дм²

Ответ: 384 дм², 672 дм²

Задача 2. В правильной n-угольной призме сторона основания равна а и высота равна h. Вычислите площади боковой и поной поверхности призмы, если: n = 6, а = 23 дм, h = 5 дм.

Дано: n = 6, а = 23 дм, h = 5 дм

Найти: S_бок–? , S_пол –?

Решение:

S_бок = 6аh
S_бок = 6· 50 · 23 = 6900 (см²) = 69 (дм²)
S_пол = 69·(100 + 23√ 3) = 69· 140 = 9660 (см²) = 97 (дм²)

Ответ: 69 дм², 97 дм²

Самостоятельное решение задач: