Контакты

Случайная статья

Лемма Даламбера.. Доказательство.

Лемма Даламбера.

Если 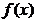- многочлен положительной степени с комплексными коэффициентами и 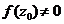для некоторог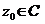о , то 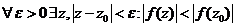(принцип минимума модуля для многочленов)

Доказательство.

Переразложим 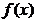по степеням : .

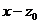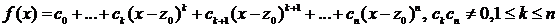По условию, .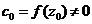

Пусть задано 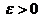; будем выбирать 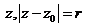исходя из неравенств: 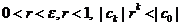. Кроме этого, обозначим углы 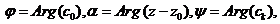тогда 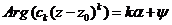. Выберем 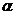так, чтобы 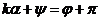, тогда и, таким образом, .

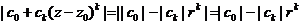Теперь обозначим 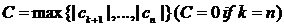и потребуем дополнительно, чтобы .

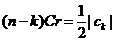Оценим 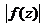: 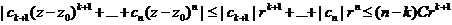и

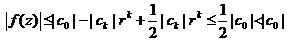, чтд.

Это доказательство – гибрид доказательств Д. А. Тимашёва и В. Т. Маркова.

. .

.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.