
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Квадратный трёхчлен и его корни
Алгебра
9 класс
Тема: Квадратный трёхчлен и его корни
Цели урока: 1) научиться выделять квадратный трёхчлен из множества других многочленов;
2) научиться находить корни квадратного трёхчлена.
Многочлен второй степени с одной переменной, имеющий вид
ax2 + bx + c, где а ≠ 0 – квадратный трёхчлен,
коэффициенты а, b и c называются также как и в квадратном уравнении:
a – первый или старший коэффициент,
b – второй коэффициент,
c – свободный член.
Пример: Среди данных многочленов найдём квадратный трёхчлен и определим его коэффициенты:
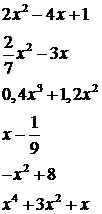 Квадратными трёхчленами будут многочлены:
1) 2x2 – 4x + 1 (а = 2, b = –4, c = 1)
2)
Квадратными трёхчленами будут многочлены:
1) 2x2 – 4x + 1 (а = 2, b = –4, c = 1)
2) 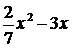 ( ( 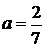 , b = –3, c = 0)
3) –x2 + 8 (а = –1, b = 0 и c = 8)
֎ Значение переменной, при котором многочлен обращается в нуль, называется корнем многочлена.
Способы нахождения корней квадратного трёхчлена:
1. Решение соответствующего квадратного уравнения:
Для того, чтобы найти корни квадратного трёхчлена аx2 + bx + c, нужно решить соответствующее квадратное уравнение: аx2 + bx + c = 0 , b = –3, c = 0)
3) –x2 + 8 (а = –1, b = 0 и c = 8)
֎ Значение переменной, при котором многочлен обращается в нуль, называется корнем многочлена.
Способы нахождения корней квадратного трёхчлена:
1. Решение соответствующего квадратного уравнения:
Для того, чтобы найти корни квадратного трёхчлена аx2 + bx + c, нужно решить соответствующее квадратное уравнение: аx2 + bx + c = 0
|
 Количество корней этого уравнения = количеству корней квадратного трёхчлена.
Количество корней этого уравнения = количеству корней квадратного трёхчлена.
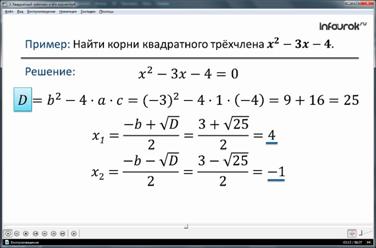 Пример: Пример:
|
Ответ: -1; 4.
2. Выделение квадрата двучлена из квадратного трёхчлена:

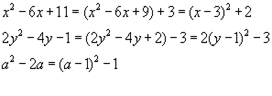 Пример:
1)
2)2x2 + 4x – 3 = 2(x2 + 2x – Пример:
1)
2)2x2 + 4x – 3 = 2(x2 + 2x –  ) = 2((x2 + 2x + 1) – 1– ) = 2((x2 + 2x + 1) – 1–  ) = 2((x + 1)2 – 1– ) = 2((x + 1)2 – 1–  ) = 2((x + 1)2 – ) = 2((x + 1)2 –  ) = 2(x + 1)2 –5. ) = 2(x + 1)2 –5.
|
| Итоги: Сегодня на уроке мы узнали - какой многочлен является квадратным трёхчленом; - два способа нахождения корней квадратного трёхчлена: 1. С помощью дискриминанта 2. С помощью выделения квадрата двучлена. ДОМАШНЕЕ ЗАДАНИЕ: 1. прочитать п. 3, знать общий вид квадратного трёхчлена; 2. найти корни квадратного трёхчлена: 1)x2 + 14x – 49; 2) 3x2 + 12x – 15; 3) -2x2-7x – 10; 4) у2 + 4у – 12. |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|