Пятнадцатое апреля. Классная работа. Приближение десятичных дробей

Пятнадцатое апреля

Классная работа

Приближение десятичных дробей

Не всегда возможно и нужно найти точные ответы на некоторые вопросы. Например, сколько кубических метров воды содержит Каспийское море? Сколько тонн снега выпало зимой? Сколько волос на голове человека? Поэтому, вместо точных берут другие значения, близкие к искомым, приближённые.

Рассмотрим несколько чисел. 1, 3; 1, 5; 1, 8

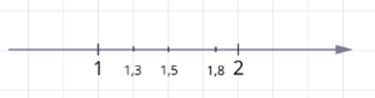
Все эти числа имеют целую часть – единицу, значит, находятся между соседними натуральными числами 1 и 2.

При этом 1, 3 находится ближе к 1, а 1, 8 ближе к 2.

Поэтому можно сказать, что 1, 3 приближённо равно 1, а 1, 8 приближённо равно 2.

Число 1, 5 находится точно в середине, его можно приблизить и к единице, и к двум.

1, 3 ≈ 1

1, 8 ≈ 2

1, 5≈ 1; 1, 5≈ 2

Но по правилам округления чисел 1, 5 ≈ 2.

Приближение десятичных дробей, которое мы выполнили, называется округлением десятичной дроби до единиц.

Округление десятичной дроби – нахождение приближённого значения.

Если число а мало отличается от числа в, то говорят, что число а приближённо равно числу в. Пишут а ≈ в (≈ – знак приближённого равенства).

Если при этом в меньше, чем а, то в называют приближением а с недостатком.

Если в больше, чем а, то его называют приближением а с избытком.

Рассмотрим на примере произвольной десятичной дроби.

а = 3, 42845

Оборвём эту дробь на цифре второго разряда после запятой.

3, 42

Получили число, меньшее, чем А.

3, 42 < а

Если увеличить число сотых на единицу, получим число, большее, чем А.

3, 43 > а

Таким образом, первоначальное число А находится между данными числами.

3, 42 < а < 3, 43

Поэтому получаем, что 3, 42 – приближение числа А с точностью до одной сотой с недостатком.

а ≈ 3, 42 с точностью до 0, 01 с недостатком.

3, 43 – приближение числа А с точностью до одной сотой с избытком.

а ≈ 3, 43 с точностью до 0, 01 с избытком.

Так как третья цифра после запятой у числа А больше пяти, то оно ближе к 3, 43, чем к 3, 42. Поэтому говорят, что 3, 43 есть приближение А с точностью до одной сотой с округлением.

Значащая цифра десятичной дроби - это первая слева направо отличная от нуля цифра, а также все следующие за ней цифры.

Например,

0, 403 – все цифры после запятой значащие.

0, 00256 – все цифры, начиная с двойки – значащие.

Округлим некоторые числа до третьей значащей цифры. Это означает, что округляем до того разряда, где находится третья значащая цифра, заменив следующие цифры нулями.

3, 14159 ≈ 3, 14000 = 3, 14

0, 046052 ≈ 0, 046100 = 0, 0461

– 0, 023039 ≈ – 0, 023000 = – 0, 0230.

№900. Найдите приближение числа а с недостатком с точностью до единицы третьего разряда после запятой:

а) а = 0, 3456

а ≈ 0, 345 – приближение с недостатком, так как 0, 345 ˂ а.

б) а = 0, 76543

а ≈ 0, 765 – приближение с недостатком, так как 0, 765 ˂ а.

г) а = - 0, 34354

а ≈ - 0, 344 – приближение с недостатком, так как - 0, 344 ˂ а.

№902. Округлите число а с точностью до 0, 01:

а) а = 1, 24851 ≈ 1, 25 (увеличили округляемый разряд на 1, так как после него стоит цифра, которая больше 5)

б)а = 1, 24158 ≈ 1, 24 (оставили округляемый разряд без изменения, так как после него стоит цифра, которая меньше 5)

в) а = -7, 02303 ≈ -7, 02

г) а = 0, 12528 ≈ 0, 13

№905(а, б) Округлите число 1995, 1996:

а) до десятых;

1995, 1996 ≈ 1995, 2

б) до сотых;

1995, 1996 ≈ 1995, 20 (после округляемого разряда стоит цифра больше 5, значит увеличиваем округляемый разряд на 1, но так как 9+1=10, а число 10 имеет 2 цифры, то на месте округляемого разряда пишем 0, а предыдущий разряд увеличиваем на 1)

Домашнее задание: чит. п. 4. 10, решить №901, 903, 905(в-е).