Добрый день!

Стр 1 из 2Следующая ⇒

Программа

Тема

Дата

Время

Содержание занятия

«Занимательное черчение»

Группа № 4

«Чертежи разверток»

29. 11. 2021-2. 12. 2021

30 мин теория за ПК

Повторение чертежей разверток

1 час практика самостоятельно

Практическая работа: Чертеж разверток

Добрый день!

Разверткой поверхности многогранника называют плоскую фигуру, полученную при совмещении с плоскостью чертежа всех граней многогранника в последовательности их расположения на многограннике.

Чтобы построить развертку поверхности многогранника, нужно определить натуральную величину граней и вычертить на плоскости последовательно все грани.

Обратите внимание, как оформляют чертежи развёрток. Над изображением пишут «Развертка» с чертой внизу. От линии сгиба, которые проводят штрихпунктирной с двумя точками, проводят линии – выноски и пишут на полке «Линии сгиба».

Развертка поверхности прямой призмы представляет собой плоскую фигуру, составленную из боковых граней – прямоугольников и двух равных между собой многоугольников оснований.

Например, у развертки поверхности правильной шестиугольной призмы все грани – равные между собой прямоугольники шириной а и высотой Н, а основания – правильные шестиугольники со стороной, равной а.

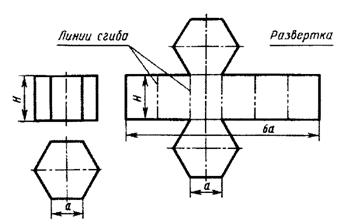Рис. 1

Таким образом, можно построить чертеж развертки поверхности любой призмы.

Аналогично строится развертка поверхности цилиндра.

Развертка поверхности цилиндра состоит из прямоугольника и двух кругов.

Одна сторона прямоугольника равна высоте цилиндра, другая – длине окружности основания. На чертеже развертки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру оснований цилиндра.

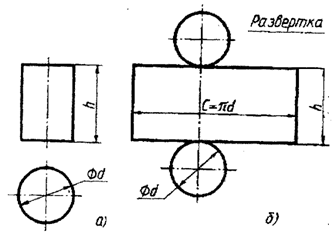
Рис. 2

Развертка поверхности правильной пирамиды представляет собой плоскую фигуру, составленную из боковых граней – равнобедренных или равносторонних треугольников и правильного многоугольника – основания.

Например, развертку поверхности правильной четырехугольной пирамиды строят так:

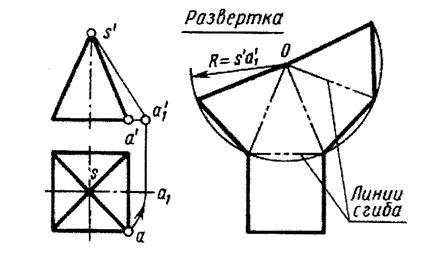
Рис. 3

Из произвольной точки О описывают дугу радиуса R , равного длине бокового ребра пирамиды. На этой дуге откладывают четыре отрезка, равные стороне основания. Крайние точки соединяют прямыми с точкой О. Затемпристраивают квадрат, равный основанию пирамиды.

Таким образом, можно построить чертежи развертки поверхности любой пирамиды.

Развертка поверхности прямого кругового конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга.

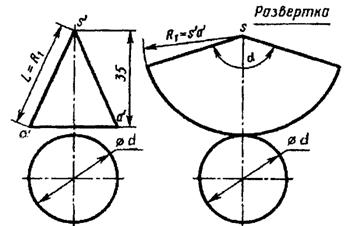
Рис. 4

Построение выполняют так:

1) Проводят осевую линию из точки S на ней описывают радиусом, равным длине S'а' = L образующей конуса, дугу окружности. На ней откладывают длину окружности основания конуса с = π d . Точку S соединяют с концевыми точками дуги.

2) К полученной фигуре – сектору пристраивают круг. Диаметр этого круга равен диаметру основания конуса.

3) Угол α подсчитывают по формул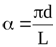е , где

d – диаметр окружности основания конуса,

L – образующая конуса.

12 Следующая ⇒