Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Конспект урока Возрастание и убывание функции. Экстремумы

Конспект урока " Возрастание и убывание функции. Экстремумы"

Повторите определение возрастающей, убывающей функций, точек минимума и максимума, наибольшего и наименьшего значений функции.

Выполните задание:

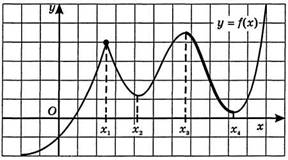
№1. По графику функции y=f(x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько промежутков возрастания у этой функции? Назовите наименьший из промежутков убывания этой функции.

Посмотрите видео https: //yandex. ru/collections/card/5e8cb3b692f20d897fae6110/

Еще раз прочитайте Теоремы 1, 2 и Теоремы 3, 4 (§44 учебника)

Обратите внимание, что для того, чтобы исследовать функцию на монотонность и экстремумы, необязательно строить график производной, достаточно определить знаки производной на промежутках, на которые стационарные и критические точки разбивают область определения функции. Фактически составляется алгоритм исследования непрерывной функции на монотонность и экстремумы:

Выполните задание

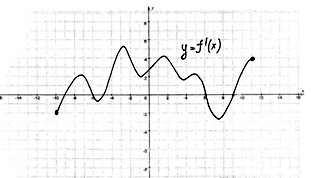
	№1. Непрерывная функция y=f(x) задана на [-10; 11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции.
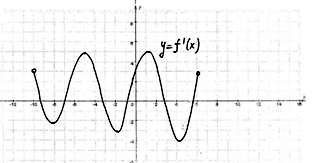
	№2. Непрерывная функция y=f(x) задана на (-10; 6). На рисунке изображён график её производной. Укажите количество точек графика этой функции, в которых касательная параллельна оси ОХ.
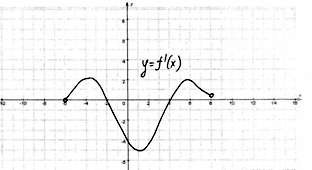
	№3. Непрерывная функция y=f(x) задана на (-6; 8). На рисунке изображён график её производной. Укажите длину промежутка убывания этой функции.
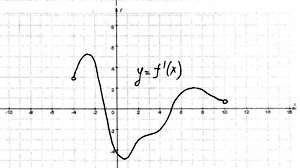
	№4. Непрерывная функция y=f(x) задана на (-4; 10). На рисунке изображён график её производной. Укажите число точек экстремума этой функции.
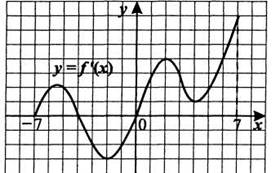
	№2. (Задание В5 ЕГЭ по математике) По графику функции y=f ´ (x) ответьте на вопросы: Сколько точек максимума имеет эта функция? Назовите точки минимума функции. Сколько промежутков возрастания у этой функции? Найдите длину промежутка убывания этой функции.

Ответы в формате №задания - ответ вышлите мне на проверку сообщением в контакте

Домашнее задание

§44, пункт 1, 2, выучить формулировки теорем и алгоритм исследование функции на монотонность и экстремумы, №44. 2, 44. 22 б, 44. 50 б, 44. 56 в.