
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теорема о конечных приращениях (теорема Лагранжа)
Теорема о конечных приращениях (теорема Лагранжа)
Теорема Лагранжа. Если функция 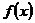 :
:
1) непрерывна на отрезке 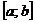 ;
;
2) дифференцируема на интервале 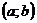 ;
;
то существует, по крайней мере, одна точка 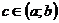 , такая, что
, такая, что
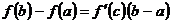 . (1)
. (1)
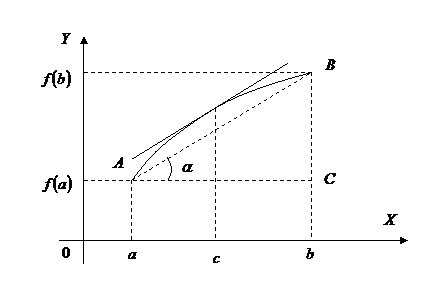
Геометрическая иллюстрация.
Из 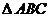 :
: 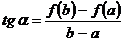 . Таким образом, если во всех точках дуги AB существует касательная, то на этой дуге найдётся точка C между A и B, в которой касательная параллельна хорде, соединяющей точки A и B.
. Таким образом, если во всех точках дуги AB существует касательная, то на этой дуге найдётся точка C между A и B, в которой касательная параллельна хорде, соединяющей точки A и B.
Пример: Проверьте, применима ли теорема Лагранжа к функции 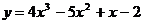 на отрезке
на отрезке 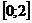 . Если окажется, что теорема применима, найдите точку c, в которой выполняется равенство (1).
. Если окажется, что теорема применима, найдите точку c, в которой выполняется равенство (1).
Решение. Функция 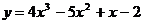 :
:
1) непрерывна на отрезке 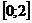 ;
;
2) дифференцируема на интервале 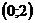 .
.
Тогда существует точка 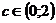 , такая, что выполняется равенство (1).
, такая, что выполняется равенство (1).
Находим значения 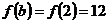 ,
, 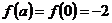 ,
, 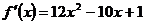 ,
, 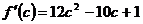 .
.
По формуле (1) получаем:
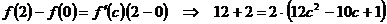
Находим корни квадратного уравнения 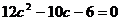 , т. е.
, т. е. 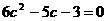 . Получаем
. Получаем 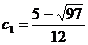 ,
, 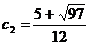 , где
, где 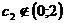 . Таким образом,
. Таким образом, 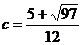 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|