Сложение и вычитание векторов. Сумма нескольких векторов - СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО - ВЕКТОРЫ В ПРОСТРАНСТВЕ

Задачи урока:

1) повторить теоретические сведения по теме, изученные в курсе планиметрии;

2) рассмотреть правила треугольника и параллелограмма сложения векторов в пространстве, законы сложения векторов;

3) обратить внимание учащихся на два способа построения разности двух векторов;

4) изучить правило сложения нескольких векторов в пространстве и его применение при нахождении векторных сумм, не прибегая к рисункам.

Ход урока

1. Повторение с целью подготовки учащихся к восприятию нового материала ответы на вопросы:

- Что называется вектором в пространстве? Его обозначения.

- Что называется длиной вектора? Ее обозначение.

- Какой вектор называется нулевым?

- Какие векторы называются коллинеарными?

- Какие векторы называются сонаправленными? Обозначение.

- Какие векторы называются противоположно направленными? Обозначение.

- Каким (сонаправленными или противоположно направленным) принять нулевой вектор?

- Какие векторы называются равными?

2. Изучение нового материала: прочитать п. 40-41. Составить конспект, выучить правила и свойства.

Примерный вид конспектов:

Сложение и вычитание векторов.

1. Сумма и разность векторов:

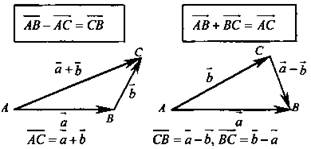2. Законы сложения векторов:

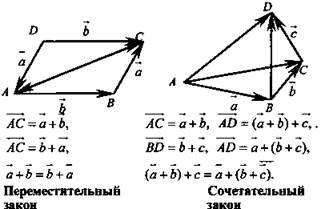
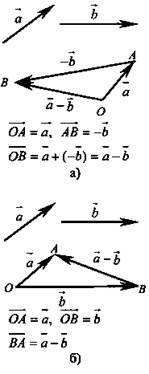
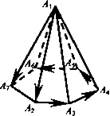
Правило многоугольника можно сформулировать также следующим образом: если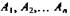

- произвольные точки, то

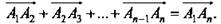Это правило проиллюстрировано на рисунке для т = 7. Отметим, что если точки А1 и Аn, то есть начало первого вектора и конец последнего, совпадают, то сумма векторов равна нулевому вектору.

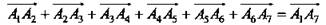
3. Закрепление изученного материала

а) Применение знаний в стандартной ситуации. Решение заданий учебника:

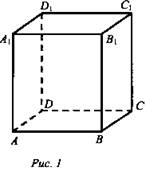
№ 327 (а, б, д) (текст - см. учебник)

(рис. 1). .

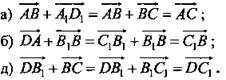
№ 328 а

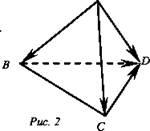
Дан тетраэдр ABCD (рис. 2).

Докажите, что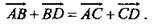

Решение: 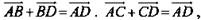следовательно,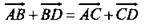

№ 331 а

Пусть ABCD — параллелограмм, а О - произвольная точка пространства.

Докажите, что 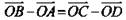(рис. 3).

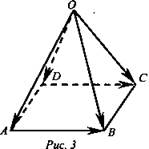
Решение: 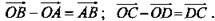Так как ABCD - параллелограмм, то 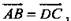следовательно, 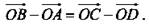В пространстве даны четыре точки А, В, С и D. Назовите вектор с началом и концом в данных точках, равный сумме векторов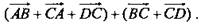

Решение: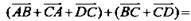

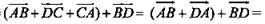
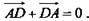
б) Самостоятельная работа обучающего характера с последующей самопроверкой (решение на обратной стороне доски)

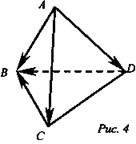
№ 379, 380 (Текст - см. учебник)

(рис. 4).

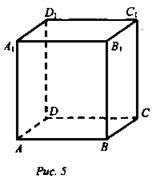
(рис. 5)

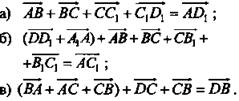
Домашнее задание

П. 40-41 прочитать, выучить правила и свойства, просмотр презентации и решение заданий «Якласс».