
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Счётные множества
Определение 1. Множество называется счётным, если оно эквивалентно множеству натуральных чисел.
A – счётно  A ~ N,
A ~ N, 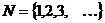
Теорема 1. Для того чтобы множество A было счётным, необходимо и достаточно, чтобы A можно было представить в виде: 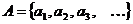 , где
, где 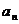 попарно различны.
попарно различны.
Доказательство:
1) Необходимость. Дано: A – счётно.  Доказать: A можно представить в виде:
Доказать: A можно представить в виде: 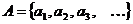 .
.
A ~ N. Пусть f биекция из N на A, обозначим:
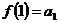 ,
, 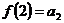 ,
, 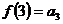 , ……
, ……
Тогда: 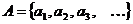 и все
и все 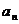 попарно различны.
попарно различны.
2) Достаточность. Дано: 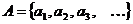
 Доказать: A – счётно.
Доказать: A – счётно.
Определим отображение 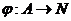 следующим образом:
следующим образом:
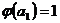 ,
,  ,
, 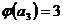 , ……
, ……
Таким образом, 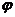 - биекция A на N.
- биекция A на N.
Следовательно, A ~ N,  A – счётно.
A – счётно.
Теорема 2. Всякое подмножество счётного множества является конечным или счётным.
Доказательство: самостоятельно (Виленкин, учебник МГЗПИ, стр. 14).
Теорема 3. Всякое бесконечное множество содержит счётное подмножество.
Доказательство: Пусть A – бесконечное множество, возьмём произвольный элемент 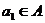 , рассмотрим
, рассмотрим 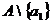 – бесконечное множество.
– бесконечное множество.
Возьмём 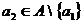 ,
,  -бесконечное множество.
-бесконечное множество.
Возьмём 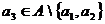 ,
, 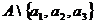 -бесконечное множество.
-бесконечное множество.
…………………………………………………………
Получим множество 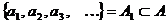 .
.
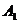 - счётно (по теореме 1) и
- счётно (по теореме 1) и 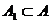 . Теорема доказана.
. Теорема доказана.
Теорема 4. Объединение конечного или счётного семейства счётных множеств является счётным множеством.
Рассмотрим счётное семейство: 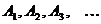 - счётные множества, докажем, что
- счётные множества, докажем, что 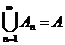 – счётно.
– счётно.
Доказательство: Так как 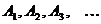 счётны, то по теореме 1 получаем:
счётны, то по теореме 1 получаем:
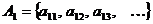
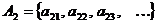
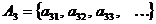
…………………………..
Будем нумеровать элементы по диагоналям.
Получим: 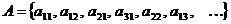 . Множество A записали в виде последовательности.
. Множество A записали в виде последовательности.
При этом, если в таблице появляется элемент ранее встречавшийся, то теперь мы его пропускаем и не записываем в последовательность.
Таким образом, A записали в виде последовательности, в которой все элементы попарно различны, следовательно, A – счётно (по теореме 1).
Теорема 5. Если к бесконечному множеству добавить конечное или счётное, то мощность множества не изменится.
Доказательство: Пусть A – бесконечное множество, B - счётное или конечное множество. Докажем, что 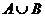 ~ A.
~ A.
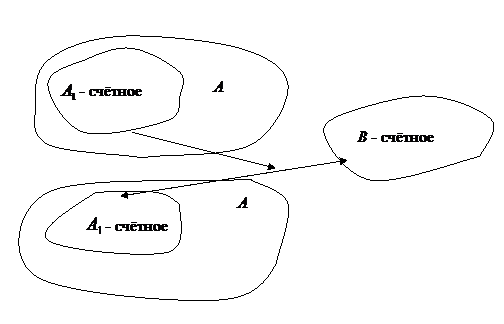
Возьмём счётное множество 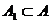 (по теореме 3), тогда
(по теореме 3), тогда 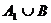 – счётное множество (по теореме 4).
– счётное множество (по теореме 4).  Существует биекция
Существует биекция 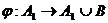 .
.
Определим отображение 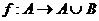 :
:

Это отображение f есть биекция.  A ~
A ~ 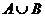 , что и требовалось доказать.
, что и требовалось доказать.
Следствие. Множество рациональных чисел счётно.
Доказательство: Представим множество рациональных чисел 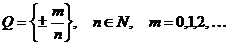 в виде объединения множеств
в виде объединения множеств 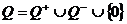 . Докажем, что множество положительных рациональных чисел
. Докажем, что множество положительных рациональных чисел 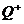 счётно.
счётно.
Пусть 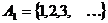 – счётное множество (по теореме 1)
– счётное множество (по теореме 1)
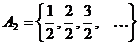 - счётное множество (по теореме 1)
- счётное множество (по теореме 1)
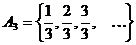 - счётное множество (по теореме 1)
- счётное множество (по теореме 1)
………………………………………………….
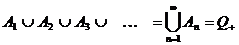 - счётное множество (по теореме 4)
- счётное множество (по теореме 4) 
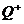 - счётное множество.
- счётное множество.
Очевидно, множество всех отрицательных рациональных чисел 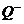 - счётно, так как
- счётно, так как 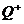 ~
~ 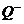 .
.
Тогда 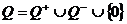 – счётное множество (по теоремам 4, 5).
– счётное множество (по теоремам 4, 5).
Определение 2. Декартовым произведением конечного семейства множеств  называется множество, элементами которого являются кортежи
называется множество, элементами которого являются кортежи 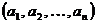 длины n, в которых
длины n, в которых 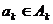 для каждого
для каждого 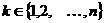 . Оно обозначается
. Оно обозначается 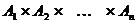 или
или 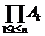 .
.
Теорема 6. Декартово произведение конечного числа счётных множеств является счётным множеством.
Дано: 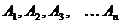 - счётные множества.
- счётные множества.  Доказать:
Доказать: 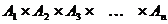 - счётно.
- счётно.
Доказательство: Доказательство проведём методом математической индукции по числу сомножителей произведения n.
1) Докажем, что 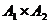 счётно (n=2).
счётно (n=2).
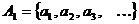 ,
,
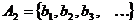 .
.
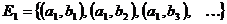 - счётное множество (по теореме 1, фиксировано
- счётное множество (по теореме 1, фиксировано 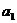 )
)
 - счётное множество (по теореме 1, фиксировано
- счётное множество (по теореме 1, фиксировано  )
)
……………………………………………………………………………………………….
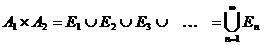
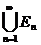 - счётно (по теореме 4)
- счётно (по теореме 4) 
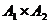 - счётно.
- счётно.
2) допустим, что утверждение выполняется для n=k. Докажем, что оно истинно для n=k+1.
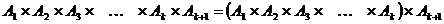
Множество 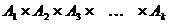 счётно по индуктивному предположению,
счётно по индуктивному предположению, 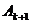 - счётно. Тогда множество
- счётно. Тогда множество 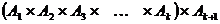 счётно как декартово произведение двух счётных множеств. Теорема доказана.
счётно как декартово произведение двух счётных множеств. Теорема доказана.
Задача. Доказать, что множество всех конечных последовательностей натуральных чисел счётно.
Доказательство: Пусть 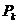 - множество всех конечных последовательностей натуральных чисел.
- множество всех конечных последовательностей натуральных чисел.
Пусть 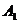 - множество последовательностей из одного элемента.
- множество последовательностей из одного элемента.
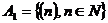 - счётно, так как
- счётно, так как 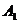 ~ N.
~ N.
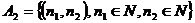 - счётно (по теореме 6), так как
- счётно (по теореме 6), так как 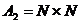 .
.
……………………………………………………………………………
Тогда 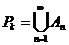 - счётно (по теореме 4).
- счётно (по теореме 4).
Определение 3. Бесконечное множество называется несчётным, если оно не является счётным.
Теорема 7. Если из несчётного множества удалить конечное или счётное, то мощность множества не изменится.
Доказательство: Пусть A - несчётное множество, B – счётное множество. Докажем, что A\B ~ B.
Обозначим A\B=C.
1) Докажем, что множество C – бесконечно.
Если бы C было конечным, что множество 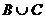 ~ B было бы счётным (по теореме 5). Но
~ B было бы счётным (по теореме 5). Но 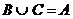 . Получаем противоречие: несчётное множество A эквивалентно счётному множеству B: A ~ B. Следовательно, C - бесконечное множество.
. Получаем противоречие: несчётное множество A эквивалентно счётному множеству B: A ~ B. Следовательно, C - бесконечное множество.
2) 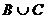 ~ C по теореме 5, но
~ C по теореме 5, но 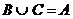
 A ~ C
A ~ C  A ~ A\B, что и требовалось доказать.
A ~ A\B, что и требовалось доказать.
Определение 4. Действительное число называется алгебраическим числом, если является корнем многочлена с целыми коэффициентами.
Любое рациональное число 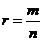 является алгебраическим, так как оно является корнем уравнения
является алгебраическим, так как оно является корнем уравнения 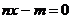 . Но среди иррациональных чисел также встречаются алгебраические, например
. Но среди иррациональных чисел также встречаются алгебраические, например 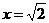 , которое является корнем уравнения
, которое является корнем уравнения 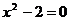 .
.
Теорема 8. Множество алгебраических чисел счётно.
Доказательство: самостоятельно (Виленкин, учебник МГЗПИ).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|