
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Радиус вписанной окружности в ромб
Радиус вписанной окружности в ромб
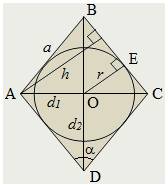
1. Выразить радиус вписанной окружности в ромб через высоту
Высота ромба равна диаметру вписанной окружности. Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.
Следовательно, формула радиуса вписанной окружности в ромб через высоту:
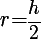
2. Выразить радиус вписанной окружности в ромб через диагонали
Площадь ромба можно выразить через радиус вписанной окружности
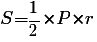 , где Р– периметр ромба.
, где Р– периметр ромба.
Зная, что периметр это сумма всех сторон четырехугольника имеем P=4× а. Тогда 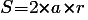
Но площадь ромба также равна половине произведения его диагоналей 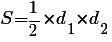 . Прировняв правые части формул площади, имеем следующее равенство
. Прировняв правые части формул площади, имеем следующее равенство 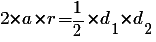
В результате получаем формулу, позволяющую вычислить радиус вписанной окружности в ромб чрез диагонали
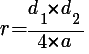
3. Выразить радиус вписанной окружности в ромб через отрезки m и n
То 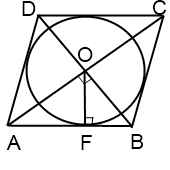 чка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF. Пусть AF=m, BF=n.
чка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF. Пусть AF=m, BF=n.
Точка O – центр пересечения диагоналей ромба и центр вписанной в него окружности.
Треугольник AOB – прямоугольный, так как диагонали ромба пересекаются под прямым углом.
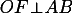 , т. к. является радиусом, проведенным в точку касания окружности. Следовательно OF – высота треугольника AOB к гипотенузе.
, т. к. является радиусом, проведенным в точку касания окружности. Следовательно OF – высота треугольника AOB к гипотенузе.
Тогда AF и BF – проекции катетов на гипотенузу.
Высота в прямоугольном треугольнике, опущенная на гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу.
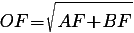
Формула радиуса вписанной окружности в ромб через отрезки равна корню квадратному из произведения этих отрезков, на которые делит сторону ромба точка касания окружности
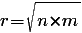
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|