Открытые и замкнутые множества

На плоскости различают открытый и замкнутый круги, открытый и замкнутый квадраты и т. д. На прямой различают открытый и замкнутый промежутки (интервал и отрезок). Разница между этими множествами состоит в том, что первые не содержат ни одной своей граничной точки, а вторые содержат все такие точки. Аналогичные классы множеств выделяют и в произвольных метрических пространствах.

Определение 1. Множество E из метрического пространства M, содержащее все свои граничные точки, называется замкнутым в M. Иными словами, E замкнуто в M в том и только том случае, когда .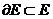

Определение 2. Множество , не содержащее ни одной своей граничной точки, называется открытым в M. Иными словами, E открыто в M тогда и только тогда, когда .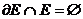

Так как точки любого множества делятся на внутренние и граничные, а открытые множества не содержат граничных точек, то все точки открытого множества внутренние.

Так как замкнутые множества не содержат внешних точек, то они содержат все свои точки прикосновения, так как только внутренние и граничные точки являются точками прикосновения.

Определение 3. Замыканием множества называется множество всех точек прикосновения множества E (обозначение [E]).

Замечание. В любом метрическом пространстве M пустое множество и само множество M являются одновременно открытыми и замкнутыми множествами.

Теорема 1. Дополнение к открытому множеству является замкнутым множеством. Дополнение к замкнутому множеству является открытым множеством.

Доказательство:

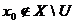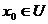1) Пусть U - открытое множество в метрическом пространстве X. Покажем, что множество X\U является замкнутым множеством, т. е. содержит все свои точки прикосновения. Действительно, если точка , то . Тогда существует окрестность 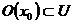, так как множество U открыто. Следовательно, 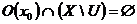, окрестность 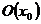не принадлежит множеству X\U, т. е. точка 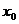не является точкой прикосновения множества X\U. Таким образом, множество X\U содержит все свои точки прикосновения.

2) Пусть теперь F - замкнутое множество в X. Докажем, что множество X\F – открытое множество, т. е. множество, все точки которого внутренние. Действительно, если 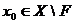, то 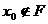, следовательно, 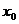не является точкой прикосновения множества F, т. к. F – замкнутое множество и содержит все свои точки прикосновения. Следовательно, должна существовать окрестность 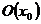, такая, что 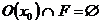. Тогда 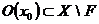, следовательно, точка 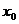- внутренняя точка множества X\F и множество X\F является открытым.

Теорема 2. Пересечение конечного семейства открытых множеств открыто. Объединение любого семейства открытых множеств открыто.

Доказательство: самостоятельно

Теорема 3. Объединение конечного семейства замкнутых множеств замкнуто. Пересечение любого семейства замкнутых множеств замкнуто.

Доказательство: самостоятельно