
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЛЕКЦИЯ 2. ОПРЕДЕЛИТЕЛИ. Ключевые понятия. 1. ОПРЕДЕЛИТЕЛИ КВАДРАТНОЙ МАТРИЦЫ И ИХ СВОЙСТВА. Пример.
ЛЕКЦИЯ 2. ОПРЕДЕЛИТЕЛИ
План
1. Определители квадратной матрицы и их свойства.
2. Теоремы Лапласа и аннулирования.
Ключевые понятия
Алгебраическое дополнение элемента определителя.
Минор элемента определителя.
Определитель второго порядка.
Определитель третьего порядка.
Определитель произвольного порядка.
Теорема Лапласа.
Теорема аннулирования.
1. ОПРЕДЕЛИТЕЛИ КВАДРАТНОЙ МАТРИЦЫ И ИХ СВОЙСТВА
Пусть А – квадратная матрица порядка n:
А= 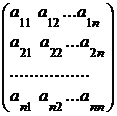 .
.
Каждой такой матрице можно поставить в соответствие единственное действительное число, называемое определителем (детерминантом) матрицы и обозначаемое
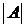 = det A= Δ =
= det A= Δ = 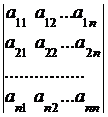 .
.
Отметим, что определитель существует только для квадратных матриц.
Рассмотрим правила вычисления определителей и их свойства для квадратных матриц второго и третьего порядка, которые будем называть для краткости определителями второго и третьего порядка соответственно.
Определителем второго порядка матрицы 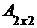 называется число, определяемое по правилу:
называется число, определяемое по правилу:
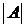 =
= 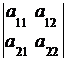 =
= 
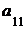
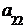 –
– 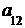
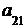 , (1)
, (1)
т. е. определитель второго порядка есть число, равное произведению элементов главной диагонали минус произведение элементов побочной диагонали.
Пример.
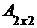 =
= 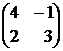 , тогда
, тогда  =
= 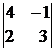 = 4 · 3 – ( –1) · 2=12 + 2 = 14.
= 4 · 3 – ( –1) · 2=12 + 2 = 14.
Следует помнить, что для обозначения матриц используют круглые или квадратные скобки, а для определителя – вертикальные линии. Матрица – это таблица чисел, а определитель – число.
Из определения определителя второго порядка следуют его свойства:
1. Определитель не изменится при замене всех его строк соответствующими столбцами:
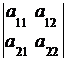 =
=  .
.
2. Знак определителя меняется на противоположный при перестановке строк (столбцов) определителя:
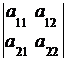 = –
= – 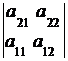 ,
, 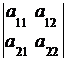 = –
= –  .
.
3. Общий множитель всех элементов строки (столбца) определителя можно вынести за знак определителя:
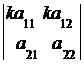 =
= 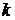
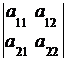 или
или 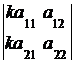 =
= 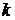
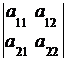 .
.
4. Если все элементы некоторой строки (столбца) определителя равны нулю, то определитель равен нулю.
5. Определитель равен нулю, если соответствующие элементы его строк (столбцов) пропорциональны:
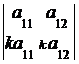 =0,
=0, 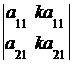 = 0.
= 0.
6. Если элементы одной строки (столбца) определителя равны сумме двух слагаемых, то такой определитель равен сумме двух определителей:
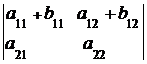 =
= 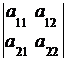 +
+ 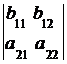 ,
, 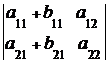 =
= 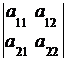 +
+ 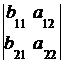 .
.
7. Значение определителя не изменится, если к элементам его строки (столбца) прибавить (вычесть) соответственные элементы другой строки (столбца), умноженные на одно и тоже число 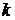 :
:
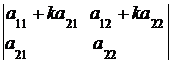 =
= 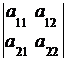 +
+ 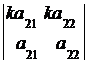 =
= 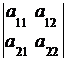 ,
,
так как 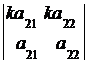 =0 по свойству 5.
=0 по свойству 5.
Остальные свойства определителей рассмотрим ниже.
Введем понятие определителя третьего порядка: определителем третьегопорядка квадратной матрицы называется число
Δ = 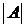 = det A=
= det A= 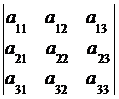 =
=
= 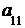
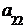
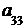 +
+ 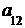
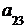
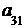 +
+ 
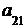
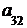 –
– 
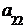
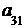 –
– 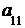
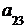
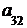 –
– 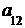
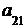
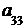 ,
,
(2)
т. е. каждое слагаемое в формуле (2) представляет собой произведение элементов определителя, взятых по одному и только одному из каждой строки и каждого столбца. Чтобы запомнить, какие произведения в формуле (2) брать со знаком плюс, а какие со знаком минус, полезно знать правило треугольников (правило Саррюса):
 |
Пример. Вычислить определитель
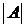 =
= 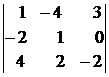 =
=
= 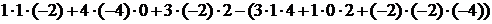 =
=
= 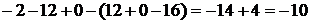 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|