Задание: изучить материал урока, выполнить самостоятельную работу и домашнее задание.

Урок

Тема: Неравенства с двумя неизвестными.

Цель: рассмотреть графический способ решения неравенств с двумя переменными и их систем

В результате обучающийся должен знать изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем.

Должен уметь решать графически неравенств с двумя переменными и их системы.

Задание: изучить материал урока, выполнить самостоятельную работу и домашнее задание.

Информационная карта

Задания

1. Решение неравенств с двумя переменными

На координатной плоскости фигуры могут задаваться неравенствами.

Графиком неравенства с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого неравенства.

Рассмотрим алгоритм построения модели решений неравенства с двумя переменными:

Записать уравнение, соответствующее неравенству.
Построить график уравнения из пункта 1.
Выбрать произвольную точку в одной из полуплоскостей. Проверить, удовлетворяют ли координаты выбранной точки данному неравенству.
Изобразить графически множество всех решений неравенства.

Рассмотрим примеры графического решения наиболее часто встречающихся неравенств с двумя переменными.

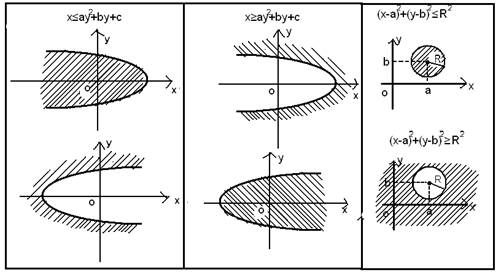
3. Графический способ решения систем неравенств с двумя переменными

Чтобы построить на координатной плоскости решение системы неравенств, надо:

1) выполнить равносильные преобразования системы так, чтобы удобно было строить графики всех неравенств, которые входят в систему;

2) построить эти графики и найти пересечение областей.

Пересечение областей представляет собой решение системы неравенств.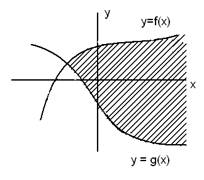

Совокупность неравенствпредставляет собой объединение этихнеравенств. Решением совокупности является всякое значение (x, y), которое обращает в истинное числовое неравенство хотя бы одно из неравенств совокупности. Множество решенийсовокупности есть объединение множеств решений неравенств, образующих совокупность.

Задача. Решить графически систему неравенств

Решение. Сначала заменяем знак неравенства знаком равенства и проводим в одной системе координат линии у = х и х² + у² = 25. Решаем каждое неравенство системы. Графиком системы будет множество точек плоскости, являющихся пересечением (двойная штриховка) множеств решений первого и второго неравенств.

Задача. Решить графически совокупность неравенств

Решение. Сначала заменяем знак неравенства знаком равенства и проводим в одной системе координат линии у = х + 4 и х2 + у2 = 16. Решаем каждое неравенство совокупности. Графиком совокупности будет множество точек плоскости, являющихся объединением множеств решений первого и второго неравенств.

12 Следующая ⇒