2.Актуализация знаний.. Определите, какие из следующих выражений являются квадратным трёхчленом; ответ объясните.

17. 11. 2020. алгебра 8 класс

Тема урока: «Квадратный трёхчлен »

Цель: восприятие и первичное осознание нового материала; изучить основные понятия, связанные с квадратным трёхчленом; вывести формулу для разложения квадратного трёхчлена на множители и формировать умение её применять.

Ход урока.

1. Организационный момент.

2. Актуализация знаний.

Устно:

Сократить дробь: ; ; ; ; ; ;

3. Объяснение нового материала:

+ + с, где - переменная, а, и с- некоторые числа, причём 0

-Это квадратный трёхчлен. Сегодня нам предстоит познакомиться с новой темой: «Квадратный трёхчлен. » (Запишите в тетради число, классная работа и тема урока)

-Дадим определение квадратного трёхчлена.

Квадратным трёхчленом называется многочлен вида

+ + с, где - переменная, а, и с- некоторые числа, причем, а 0

Задание:

Определите, какие из следующих выражений являются квадратным трёхчленом; ответ объясните.

а) 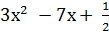+ б) - в) +

г) 2х – 1, 27 - д) +

Заметим, что значение квадратного трёхчлена зависит от значения х. Например,

Если х = 0, то

Если х = 2, то

Если х = -1, то

При х = -1 квадратный трёхчлен обращается в нуль, в этом случае число -1 называют корнем квадратного трёхчлена.

-Сформулируем определение корня квадратного трёхчлена.

Определение. Корнем квадратного трёхчлена называется значение переменной, при котором значение этого трёхчлена равно нулю.

- Как отыскать корни квадратного трёхчлена?

Приравнять к нулю трёхчлен и найти дискриминант.

-Итак, появилось новое понятие дискриминант квадратного трёхчлена

Определение. Дискриминантом квадратного трёхчлена + + с называется значение выражения D = b² – 4 с.

Пример: учебник стр 70

4. Формирование умений и навыков:

№200, 201

№202(1, 3 столб), 203(а, л, и)

5. Итог.

7. Домашнее задание. П. 4. 1 до теоремы 2,   №202(2 столб), 203(д, к, м)

Мне фотоотчёты.

Если    D

Если D , то квадратный трёхчлен имеет 1 корень или 2 равных корня;

Если D , то квадратный трёхчлен не имеет корней.

Вы умеете составлять квадратное уравнение, если известны корни, а квадратный трёхчлен - это его левая часть. Нам предстоит выполнить обратную работу. Посмотрите на работу ученика, работающего по карточке №1:

(х-3)(х-2) = - 5 +6

Поменяем местами левую и правую части этого равенства

- 5х +6 = (х-3)(х-2)

Вывод: получилось, что трёхчлен разложен на множители, а 2 и 3 это корни квадратного трёхчлена.

-Рассмотрим другой трёхчлен 2 - 10х + 12. Как его разложить на множители?

2 - 10х + 12 = 2( - 5х +6) = 2(х-3)(х-2), где а = 2 – первый коэффициент.

Запишем в общем виде: + + с = (х - )(х - ), где и корни квадратного трёхчлена + + с.

-Мы получили разложение квадратного трёхчлена на множители. Откроем страницу 136 учебника. Читаем вслух правило в рамочке. (слайд 6)

Если и   корни квадратного трёхчлена + + с,

то + + с = (х - )(х - )

  Наш вывод совпал с выводом учебника.

Это можно доказать перемножив множители правой части. В учебнике есть доказательство. Кто желает рассмотреть доказательство дома и на следующем уроке показать его нам? (слайд 7)

Итак, если квадратный трёхчлен имеет корни, то он раскладывается на множители. Читаем обратное утверждение:

Если квадратный трёхчлен раскладывается на линейные множители, то он имеет корни. По - другому, читаем в книге стр. 137 в рамке

Если квадратный трёхчлен не имеет корней, то его нельзя разложить на линейные множители.