Задачи отборочного этапа прошлых лет на курс «Олимпиадная математика» для ребят, завершивших 10 класс

Задачи отборочного этапа прошлых лет на курс «Олимпиадная математика» для ребят, завершивших 10 класс

1. Решите уравнение 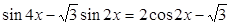. Укажите его корни, удовлетворяющие условию .

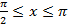2. Найдите сумму целых решений неравенства 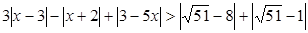, принадлежащих отрезку [-15; 16].

3. Сколькими способами можно выбрать из колоды в 36 карт две карты одного достоинства?

4. Докажите, что медианы треугольника пересекаются в одной точке. Найдите расстояние от этой точки до вершины наибольшего угла в треугольнике со сторонами 5, 12 и 13.

5. При каких значениях параметра а неравенство 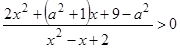выполняется для всех неотрицательных значений x?

6. Решите уравнение .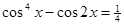

7. Найдите все значения х, при каждом из которых произведение значений выражени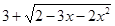й и 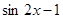отрицательно.

8. Сколькими способами можно составить из 8 детей два хоровода вокруг новогодней ёлки, если каждый хоровод должен включать как минимум три ребенка?