Задачи отборочного этапа прошлых лет на курс «Олимпиадная математика» для ребят, завершивших 8 класс

1. Докажите, что число 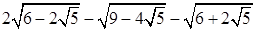- целое.

2. В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота СН. Найдите АН, если АС=15, АВ=50.

3. В равнобокой трапеции диагональ перпендикулярна боковой стороне и является биссектрисой острого угла при основании. Найдите высоту трапеции, если ее площадь равна 9 . (Площадь трапеции вычисляется по формуле 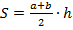, где a и b - основания трапеции, h – высота трапеции. )

4. После смешивания двух растворов кислоты, первый из которых содержал 36 г, а второй 27 г чистой кислоты, получили раствор общей массой 450 г. Найдите массу каждого из первоначальных растворов, если разность концентраций первого и второго растворов была 15%.

5. В 11-значном числе 27149103**2 две неизвестные цифры обозначены звездочками. Восстановите их, зная, что число без остатка делится на 36. Ответ обоснуйте.

6. Решите систему неравенств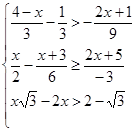

7. Расстояние между двумя городами 360 км. Из этих городов навстречу друг другу выезжают одновременно два автомобиля и встречаются через 2 часа. Они могут встретиться на середине пути, если первый выедет на 27 мин. раньше второго. Найдите скорость первого автомобиля.

8. В прямоугольном треугольнике АВС известны катет АС=4 и гипотенуза АВ=8. Найдите 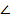АОВ, если О – центр вписанной в треугольник окружности.

9. В параллелограмме АВСК диагонали пересекаются в точке М. Известны периметры следующих треугольников: АВМ – 5 см, ВМС – 8 см, АВС – 12 см и АВК – 10 см. Найдите периметр параллелограмма.

10. Вычеркните в числе 52582241 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите наибольшее из таких получившихся после вычеркивания чисел. Приведите объяснения.