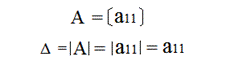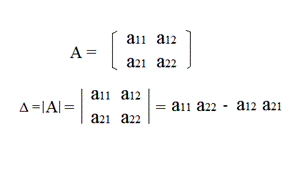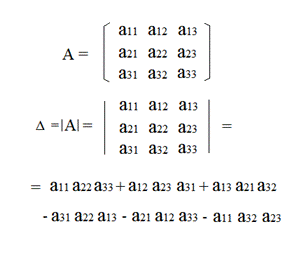Свойства определителей.

определитель матрицы - это число, характеризующее матрицу (параметр). Для каждой квадратной матрицы можно рассчитать число по ее элементам по определенной формуле, которое будет ее характеризовать.
	Для матрицы первого порядка определитель равен элементу а11.
	Для матрицы второго порядка определитель равен разности произведений элементов матрицы, рассчитанный по формуле:
	Для матрицы третьего порядка определитель равен числу, рассчитанному по формуле:
Свойства определителей.
		1. При транспонировании определитель не меняется. 2. Если поменять местами любые две строки (столбца) матрицы, то определитель поменяет знак на противоположный. 3. Для любой матрицы, определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения. 4. Определитель равен нулю, если матрица содержит две одинаковые строки (столбца). 5. Определитель равен нулю, если все элементы какой-либо строки (столбца) равны нулю. 6. Если суммировать произведения элементов любой строки (столбца) на алгебраические дополнения элементов любой другой строки (столбца), то определитель равен нулю. 7. Общий множитель любой строки (столбца) можно вынести за знак определителя.

12 3 Следующая ⇒