10 класс. Геометрия. Тема: Параллельность прямой и плоскости

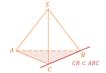Первый случай. Прямая лежит в плоскости, т. е. каждая точка прямой лежит в плоскости. Например, если SABC – треугольная пирамида, то прямая CB лежит в плоскости ABC.

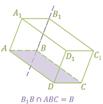
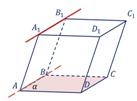Второй случай. Прямая и плоскость пересекаются, т. е. имеют только одну общую точку. Например, прямая B₁B пересекается с плоскостью грани ABCD параллелепипеда ABCDA₁B₁C₁D₁.

И третий случай. Прямая и плоскость не имеют ни одной общей точки. Например, если ABCDA₁B₁C₁D₁– куб, то прямая A₁D₁и плоскость, в которой лежит грань ABCD, не пересекаются.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Параллельность прямой а и плоскости α обозначается следующим образом 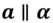. Читают: «Прямая a параллельна плоскости α ».

Отрезок (луч) называется параллельным плоскости, если он лежит на прямой, параллельной данной плоскости.

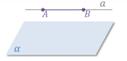
Приведем несколько примеров параллельности прямой и плоскости.

Вот возьмем, к примеру, гитару. Натянутая гитарная струна и плоскость грифа параллельны. Линии электропередач параллельны плоскости земли.

Еще примером может послужить линия пересечения стены и потолка. Эта линия параллельна плоскости пола.

Прямые о которых мы сейчас говорили, обозначены буквами а и b. Оказывается, что если в плоскости α имеется прямая b, параллельная прямой а, не лежащая в плоскости α, то прямая а и плоскость α параллельны.

Это утверждение (теорема) является признаком , по которому можно сделать вывод о параллельности прямой а и плоскости α.

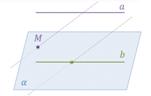Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

На рисунке изображен параллелепипед ABCDA₁B₁C₁D₁. Прямая A₁B₁ параллельна плоскости α, в которой лежит грань ABCD. Действительно, прямая A₁B₁ параллельна прямой AB, лежащей в плоскости α. Следовательно, по признаку параллельности прямой и плоскости A₁B₁ параллельна α.

Докажем еще два утверждения, которые часто применяются при решении задач.

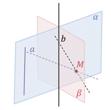Первое утверждение. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Докажем это утверждение. Пусть плоскость α проходит через прямую а, параллельную плоскости β. И плоскости α и β пересекаются по прямой b. Докажем, что прямая а параллельна прямой b.

Действительно, эти прямые лежат в одной плоскости (в плоскости α ) и не пересекаются: ведь в противном случае, если бы прямые а и b пересекались в некоторой точке М, тогда бы прямая а пересекала плоскость β в точке М. Что невозможно, поскольку прямая а параллельна плоскости β по условию.

Таким образом, прямые а и b параллельны. Что и требовалось доказать.

Второе утверждение. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Доказательство. Пусть прямые а и b параллельны. Причем прямая а параллельна плоскости α. Тогда прямая а не пересекает плоскость α, и, следовательно, по лемме о пересечении плоскости параллельными прямыми прямая b также не пересекает плоскость α. А значит, прямая b либо параллельна плоскости α, либо лежит в этой плоскости. Что и требовалось доказать.

Задача. Прямая 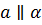. Точка 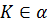. Докажите, что прямая, проходящая через точку 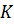и параллельная прямой 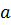, лежит в .

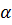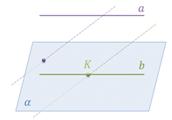Доказательство. Пусть прямая b проходит через точку K и параллельна прямой а.

Предположим, что прямая b не лежит в плоскости α, т. е. пересекает плоскость α в точке К. Тогда прямая а также пересекает плоскость α по лемме о пересечении плоскости параллельными прямыми. А это противоречит условию. Следовательно, прямая b лежит в плоскости α. Что и требовалось доказать.

1. Изучите материал урока, выучите и выпишите теоремы п. 6

2. Выполнить тренировочные упражнения №4, 10, 12

на сайте https: //resh. edu. ru/subject/lesson/6065/train/125667/ и записать с помощью математических символов их решение в тетрадь.