Параллелограмм, его признаки.

Признак I

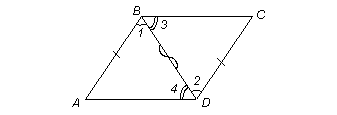Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник параллелограмм.

Дано: ABCD – четырехугольник. AB = CD, AB || CD.

Доказать: ABCD – параллелограмм.

Доказательство:

I) Д. П. – диагональ BD.

II) 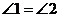, как накрест лежащие углы при параллельных прямых AB и CD и секущей BD.

III) Рассмотрим 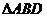и .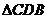

1) АВ = СD (по условию).

2) 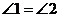(по доказанному во II-м).

3) ВD – общая.

Из условий 1), 2), 3) получаем, что 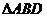= 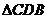по 2-м сторонам и углу между ними. В равных треугольниках напротив равных сторон лежат равные углы. Значит, .

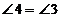IV) 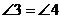– накрест лежащие углы при прямых BC и AD и секущей BD, значит, BС || АD.

V) AB || CD (по условию), BС || АD (по доказанному в IV-м), тогда ABCD – параллелограмм по определению.

Что и требовалось доказать.

Признак II

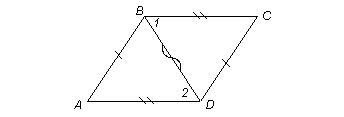Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник параллелограмм.

Дано: ABCD – четырехугольник. AB = CD, BС = АD.

Доказать: ABCD – параллелограмм.

Доказательство:

I) Д. П. – диагональ BD.

II) Рассмотрим 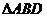и .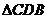

1) АВ = СD (по условию).

2) АD = ВС (по условию).

3) ВD – общая.

Из условий 1), 2), 3) получаем, что 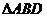= 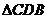по 3-м сторонам. В равных треугольниках напротив равных сторон лежат равные углы. Значит, .

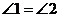III) 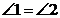– накрест лежащие углы при прямых BC и AD и секущей BD, значит, BС || АD.

IV) BС || АD (по доказанному в III-м), BС = АD (по условию), тогда ABCD – параллелограмм по I-му признаку параллелограмма.

Что и требовалось доказать.

Признак III

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм.

Дано: ABCD – четырехугольник. AB и ВD – диагонали. 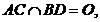AO = OC, BO = OD.

Доказать: ABCD – параллелограмм.

Доказательство:

I) Рассмотрим и .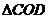

1) 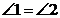(т. к. вертикальные углы).

2) ВО = OD (по условию).

3) AО = OC (по условию).

Из условий 1), 2), 3) получаем, что = 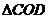по 2-м сторонам и углу между ними. В равных треугольниках напротив равных сторон лежат равные углы, а напротив равных углов лежат равные стороны. Значит, 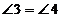, АВ = CD.

II) 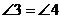– накрест лежащие углы при прямых АВ и СD и секущей BD, значит, АВ || СD.

III) АВ = CD (по доказанному в I-м), АВ || СD (по доказанному во II-м), тогда ABCD – параллелограмм по I-му признаку параллелограмма.