
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
11 класс Алгебра
11 класс Алгебра
Дата 07. 02
" Площадь криволинейной трапеции и интеграл "
Посмотрите видео: https: //www. youtube. com/watch? v=bYGRqjMqikw
Прочитайте параграф 56 и выпишите основной материал
Разберите материал урока
Выполните задания №1000(1, 3), №1003(1)
Рассмотрим фигуру, которая ограничена снизу отрезком 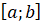 оси
оси 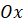 . Сверху ограничена графиком непрерывной функции
. Сверху ограничена графиком непрерывной функции 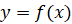 такой, что
такой, что 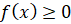 при
при 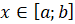 и
и 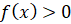 при
при  . С боков фигура ограничена отрезками прямых
. С боков фигура ограничена отрезками прямых 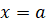 и
и 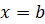 . Эту фигуру называют криволинейной трапецией.
. Эту фигуру называют криволинейной трапецией.
Отрезок 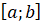 называют основанием этой криволинейной трапеции.
называют основанием этой криволинейной трапеции.
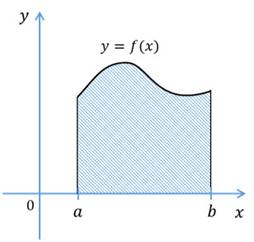
Площадь криволинейной трапеции можно вычислить по формуле 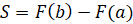 , где
, где 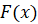 – любая первообразная функции
– любая первообразная функции 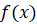 .
.
Получается, что вычисление площади криволинейной трапеции сводится к отысканию первообразной 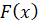 функции
функции 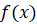 , то есть к интегрированию функции
, то есть к интегрированию функции 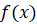 .
.
Разность 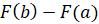 называют интегралом от функции
называют интегралом от функции 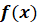 на отрезке
на отрезке 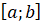 и обозначают
и обозначают 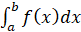 . Читается: «Интеграл от А до БЭ ЭФ от икс ДЭ икс», то есть можно записать формулу
. Читается: «Интеграл от А до БЭ ЭФ от икс ДЭ икс», то есть можно записать формулу 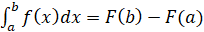 .
.
Эту формулу называют формулой Ньютона – Лейбница в честь создателей дифференциального и интегрального исчисления: Исаака Ньютона и Готфрида Вильгельма Лейбница.
Обратите внимание, что правую часть формулы часто записывают вот таким образом: 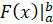 . В таком случае формула примет вид
. В таком случае формула примет вид 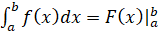 .
.
Числа 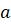 и
и 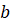 называют соответственно нижним и верхним пределами интегрирования. Функцию
называют соответственно нижним и верхним пределами интегрирования. Функцию 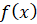 называют подынтегральной функцией. Переменную
называют подынтегральной функцией. Переменную 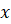 называют переменной интегрирования.
называют переменной интегрирования.
Далее из двух формул мы получаем, что 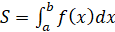 .
.
Пример. Давайте с вами вычислим площадь криволинейной трапеции, ограниченной графиком функции 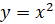 , осью
, осью 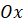 и прямыми
и прямыми 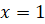 и
и 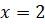 .
.

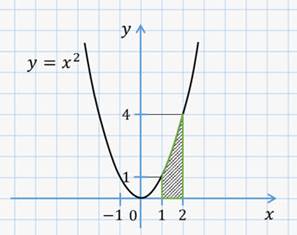
Пример. Найдём площадь криволинейной трапеции, изображённой на рисунке.
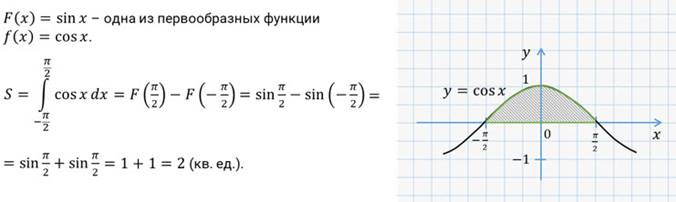
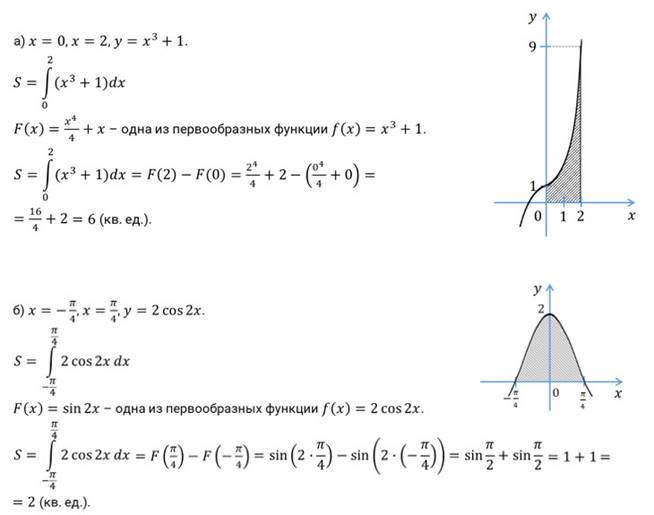
Пример. Найдите площадь криволинейной трапеции, ограниченной прямыми 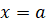 ,
, 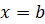 , осью
, осью 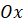 и графиком функции
и графиком функции 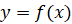 :
:
) 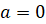 ,
, 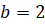 ,
, 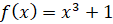 ; б)
; б) 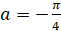 ,
, 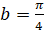 ,
, 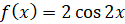 .
.
Решение.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|