
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение задач. Задача 573.. Задача 575.
Решение задач
Задача 573.
Точки А и В лежат на сфере с центром О, О не лежит на отрезке АВ. Доказать, что если М — середина отрезка АВ, то ОМ┴ АВ.
Доказательство:
1. АО=ОВ как радиусы, АМ=МВ — по условию, тогда треугольник АОВ – равнобедренный.
2. Отрезок ОМ — медиана треугольника АОВ.
В равнобедренном треугольнике медиана, проведённая к основанию, является высотой, поэтому ОМ┴ АВ. Таким образом, мы доказали, что если М — середина отрезка АВ, то ОМ┴ АВ.
Задача 575.
Точки А и В лежат на сфере радиусом R. Найти расстояние от центра сферы до прямой АВ, если АВ=m.
Решение:
1. Дополнительное построение: проведём плоскость через точки А, В и О (центр сферы).
В сечении получим окружность радиуса r.
2. Треугольник АОВ — равнобедренный, так как АО и ОВ — радиусы.
Дополнительное построение: проведём высоту ОМ, которая является и медианой.
ОМ — искомое расстояние от центра сферы до прямой АВ.
Найдём его.
3. Поскольку АВ=m, ОМ — медиана, то
МА=МВ= 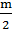
4. Найдём ОМ из прямоугольного треугольника АОМ по теореме Пифагора:
ОМ= 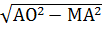 =
= 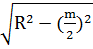 =
= 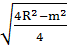 . Итак, расстояние от центра сферы до прямой АВ равно
. Итак, расстояние от центра сферы до прямой АВ равно 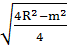 .
.
Домашнее задание: стр. 140-141, п. 64, № 574(а, в, г).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|