Хелпикс

Главная

Контакты

Случайная статья



Упражнение 7. Показатели качества САР



Упражнение 7

Показатели качества САР

Смысл всякого управления есть в переводе объекта из одного состояния в другое. Как проходит этот процесс можно вычислить, если САР задана и известно входное воздействие. Процесс перехода из одного состояния в другое называют переходным. Характер переходного процесса определяет качество системы управления.

Цель работы: построение переходной характеристики и определение

показателей качества системы.

Дано: передаточная функция разомкнутой системы, входное воздействие.

Задание: 1. Построить график выходной величины и определить прямые оценки качества;

           2. Найти степень устойчивости η, колебательность μ, значение ξ, время переходного процесса tη , затухание ζ;

           3. Определить существует ли запас устойчивости;

 

Прямые оценки качества получают по кривой переходной характеристики 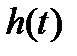, т. е. при воздейст­вии единичной ступенчатой функции и нулевых начальных условиях.  

Эту характеристику можно построить для выходной вели­чины (рис. 1).

Рис. 1. Переходная характеристика 

К прямым оценкам качества относят:

1. Время регулирования 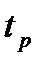— минимальное время, по ис­течении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью

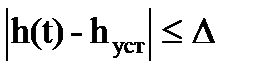
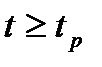
где ∆ — постоянная величина, значение которой нужно ого­варивать (задается величина ∆ в процентах от установившего­ся значения выходной величины( ).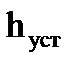

2 Перерегулирование: .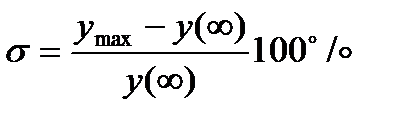

    Допустимое значениеперерегулирования зависти от назначения системы и определяется на основании эксплуатации подобных систем. Для электрических систем 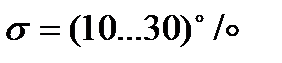 считается вполне приемлемым однако для систем управления станками - автоматами, химическими и ядерными реакторами какое-либо перерегулирование совершенно недопустимо.

где 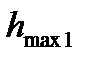— значение первого максимума.

3. Частоту колебаний 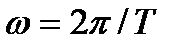, где Т — период колеба­ний для колебательных переходных характеристик.

4. Число колебаний n, которое имеет переходная характе­ристика 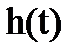 за время регулирования .

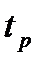5. Время достижения первого максимума .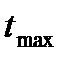

6. Время нарастания переходного процесса 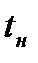— абсцис­су первой точки пересечения кривой переходной характери­стики 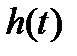с уровнем установившегося значения .

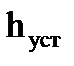7. Декремент затухания 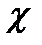, равный отношению модулей двух смежных перерегулирований:

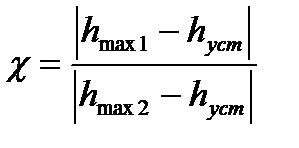
Для приближенной оценки качества переходного процесса в системе нужно на плоскости корней s выделить область, в которой располагаются

Для приближенной оценки качества переходного процесса в системе нужно на плоскости корней s выделить область, в которой располагаются корни ее харак­теристического уравнения. Чаще всего эту область представляют трапецией (рис. 2).

Корни характеристического уравнения располагаются внутри этой трапеции, на ее сторонах и ос­нованиях хотя бы по одному корню, а вне ее — ни одного. После построения трапеции на плоскости корней вычисляют параметры:

 ---степень устойчивости η,

---колебательность μ,

 ---значение ξ веществен­ной части максимально удаленного кор­ня от мнимой оси(V)

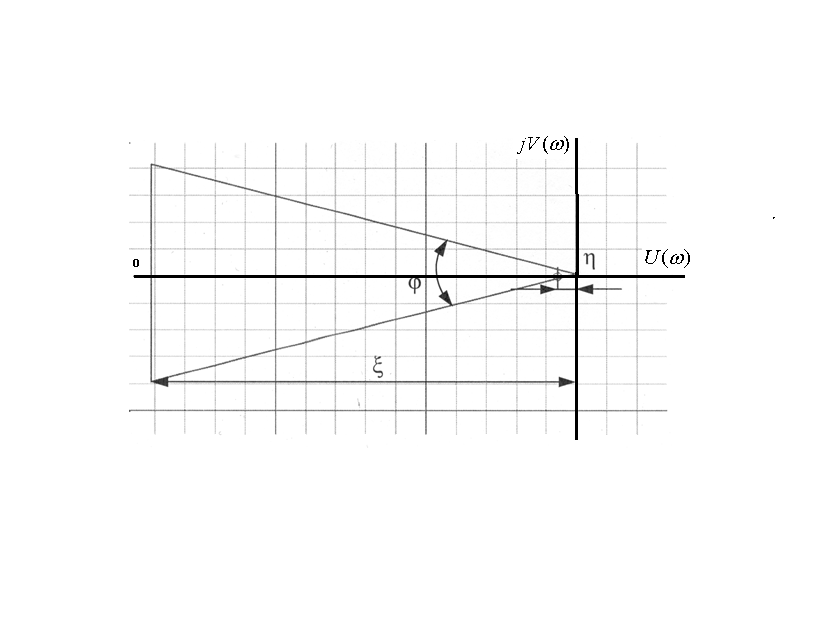
Рис. 2. Область расположения

                               корней харак­теристического уравнения

Степенью устойчивостиη называют рас­стояние от мнимой оси до ближайшего корня или ближайшей пары сопряженных комплексных корней. Степень устойчиво­сти η определяет ближайшее к мнимой оси основание трапеции(рис. 2).

Колебательностью системы μ называют тангенс угла, об­разованного отрицательной вещественной полуосью и лучом из начала координат к корню, у которого отношение мнимой ча­сти к действительной максимально (рис. 2):

,

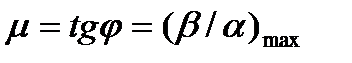где β — значение мнимой части корнейD(s); α — действи­тельная часть.

Колебательность связана с другим корневым показателем запаса устойчивости – затуханием:

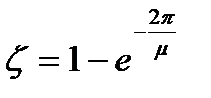
 Варианты заданий.

№ Передаточная функция Параметры
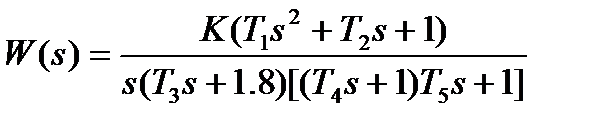
К=26. 7; Т1=0. 04с; Т2=0. 005с; Т3=0. 37с; Т4=1. 42с; Т5=0. 49с
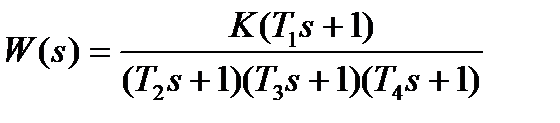
К=20. 0; Т1=0. 02с; Т2=0. 0025с; Т3=0. 01с; Т4=2. 71с
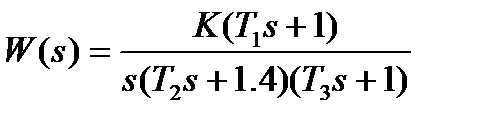
К=13. 3; Т1=0. 02с; Т2=0. 021с; Т3=0. 01с
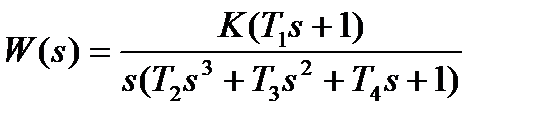
К=20. 0; Т1=0. 1с; Т2=0. 0003с; Т3=0. 067с; Т4=2. 47с
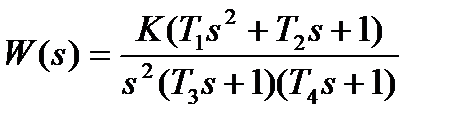
К=40. 0; Т1=0. 2с; Т2=0. 025с; Т3=0. 006с; Т4=2. 81с
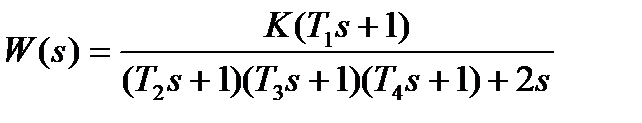
К=49. 7; Т1=0. 5с; Т2=0. 5с; Т3=0. 12с; Т4=0. 25с
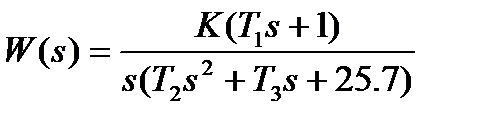
К=103; Т1=0. 075с; Т2=0. 1с; Т3=0. 32с
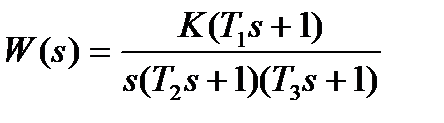
К=20. 0; Т1=0. 02с; Т2=0. 03с; Т3=0. 49с
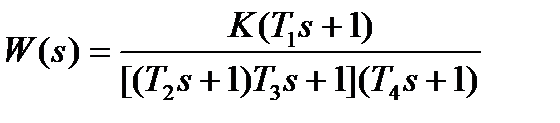
K=4; T1=0. 044с; T2=0. 133с; T3=0. 12с; Т4=0. 25с
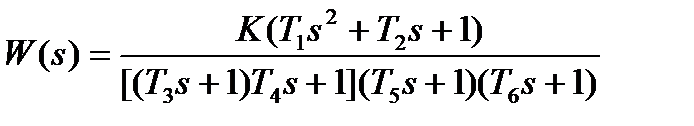
K=30; T1=0. 1с; T2=0. 3с; T3=0. 1с; T4=0. 17с; Т5=0. 15с; Т6=0. 25с
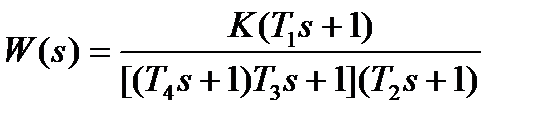
K=16; T1=0. 094с; T2=0. 44с; T3=0. 1с; Т4=0. 25с

 

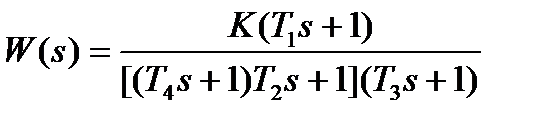
K=54; T1=0. 2с; T2=0. 03с; T3=0. 04с; Т4=0. 05с.
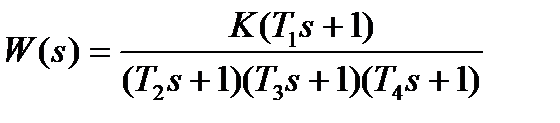
K=7. 5; T1=0. 14с; T2=0. 002с; T3=0. 03с; Т4=0. 2с
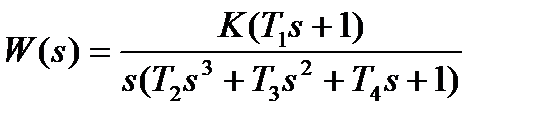
  К=5. 0; Т1=0. 004с; Т2=0. 008с; Т3=0. 104с;
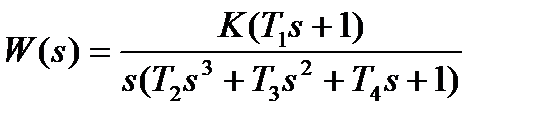
К=25; Т1=0. 002с; Т2=0. 012с; Т3=0. 004с; Т4=0. 17с
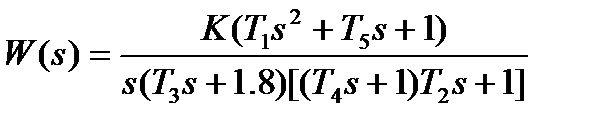
К=28. 7; Т=0. 03с; Т2=0. 007с; Т3=0. 4с; Т4=1. 4с; Т5=0. 5с
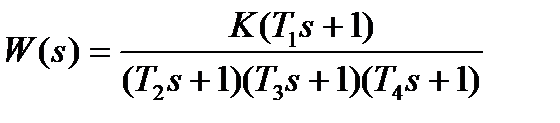
К=25. 0; Т1=0. 04с; Т2=0. 003с; Т3=0. 05сТ4=2. 7с
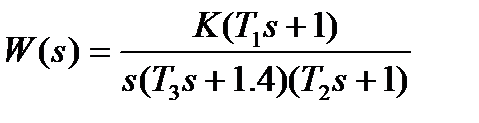
К=13; Т1=0. 07с; Т2=0. 02с; Т3=0. 04с
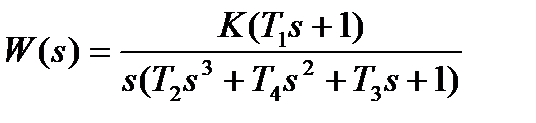
К=28; Т1=0. 3с; Т2=0. 0009с; Т3=0. 07с; Т4=2. 4с
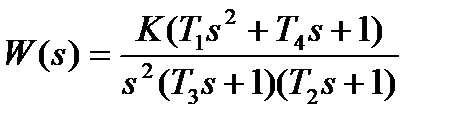
К=47. 0; Т1=0. 7с; Т2=0. 04с; Т3=0. 008с; Т4=2. 8с
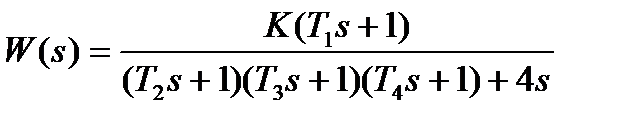
К=50; Т1=0. 8с; Т2=0. 4с; Т3=0. 1с; Т4=0. 2с
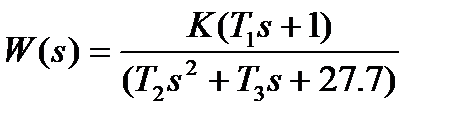
К=105; Т1=0. 08с; Т2=0. 5с; Т3=0. 3с
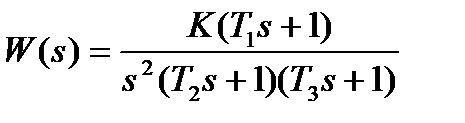
К=30. 0; Т1=0. 08с; Т2=0. 05с; Т3=0. 4с
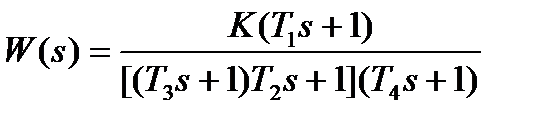
K=14; T1=0. 04с; T2=0. 13с; T3=0. 1с; Т4=0. 2с
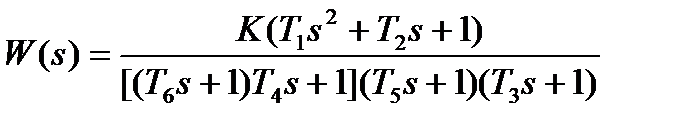
K=32; T1=0. 3с; T2=0. 5с; T3=0. 4с; T4=0. 2с; Т5=0. 1с; Т6=0. 35с
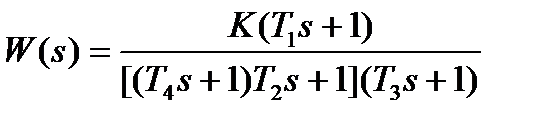
K=18; T1=0. 09с; T2=0. 4с; T3=0. 2с; Т4=0. 1с
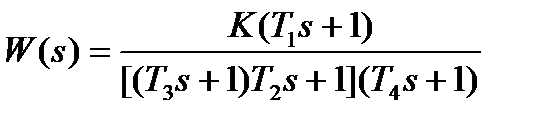
K=74; T1=0. 5с; T2=0. 07с; T3=0. 05с; Т4=0. 03с
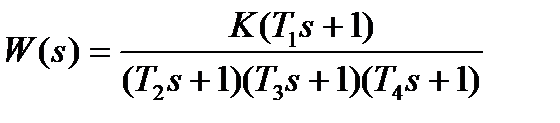
K=25; T1=0. 18с; T2=0. 005с; T3=0. 07с; Т4=0. 4с
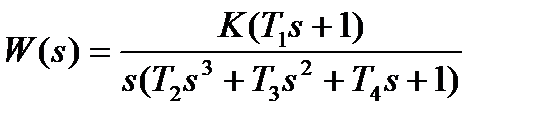
К=7. 0; Т1=0. 009с; Т2=0. 007с; Т3=0. 13с; Т4=1. 5с
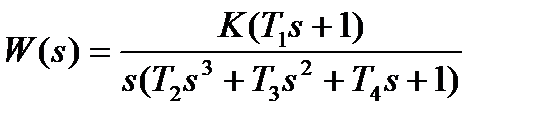
К=45; Т1=0. 008с; Т2=0. 05с; Т3=0. 003с; Т4=0. 2с

Порядок выполнения задания.

1. Найти корни характеристического уравнения. По знаку вещественной части корней определить устойчива система или нет.

2. По теореме разложения найти аналитическое выражение выходной величины  (пример) и построить ее график (рис. 1). По графику определить прямые оценки качества и тип переходного процесса.

 3. По корням характеристического уравнения системы построить область корней (трапецию). По трапеции (рис. 2) определить: степень устойчивости η, колебательность μ, значение ξ, время переходного процесса tη

4. Построить на одном графике кривые , мажоранту и миноранту в относительном времени   и определить затухание ζ (рис. 3).

5. Найти значениепоказателя колебательности М, построив график (рис. 4).

Пример. Найти закон изменения выходной величины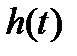

замкнутой следящей системы при входном воздействии 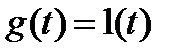 и нулевых начальных условиях.

Передаточная функция разомкнутой системы:

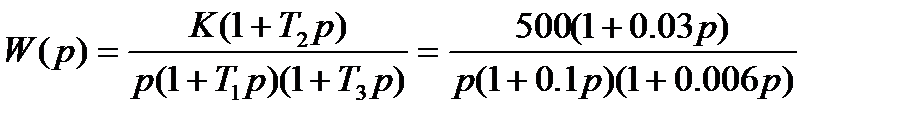
    Находим передаточную функцию замкнутой системы:

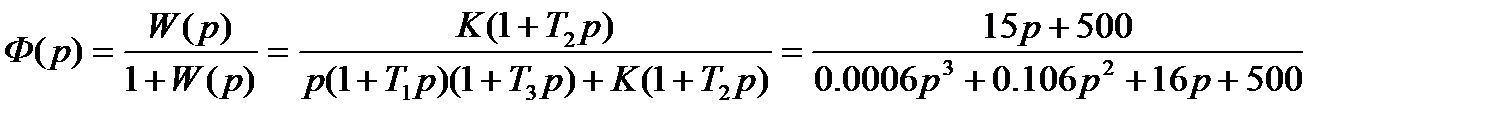
     Характеристическое уравнение замкнутой системы                                            

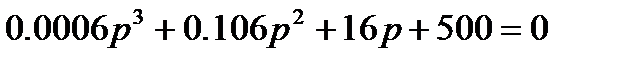
Находим корни характеристического уравнения:

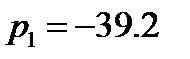
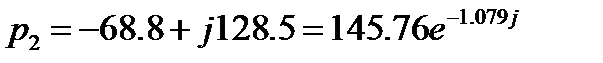
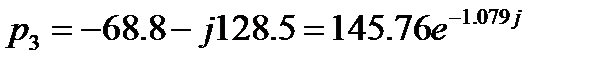
Пусть искомая функция 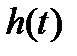 имеет изображение:

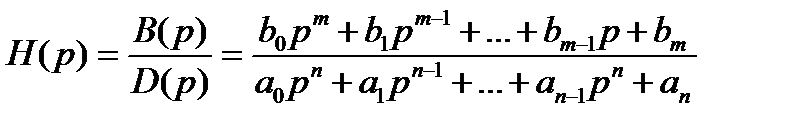
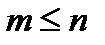
D(p) – не имеет нулевых и кратных корней. Тогда, согласно теореме разложения, оригинал 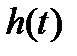 может быть найден по формуле:

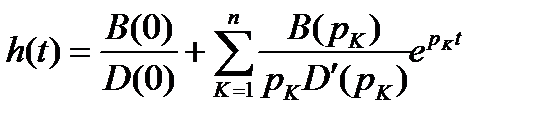
где 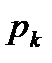 – корни характеристического уравнения

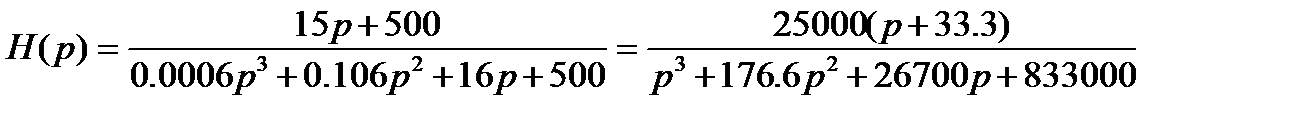
Находим:

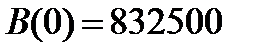
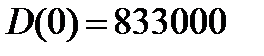
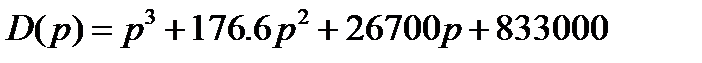
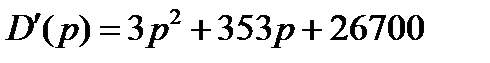
Согласно теореме разложения

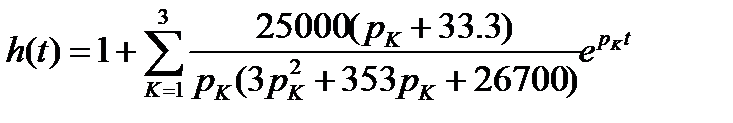(1)

  Вычислим отдельно слагаемые, находящиеся в (1) под знаком суммы.

При 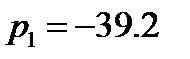получим

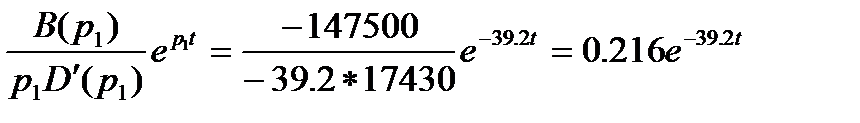(2)

При 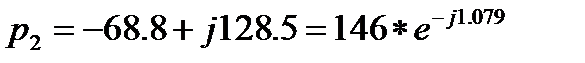 получим:

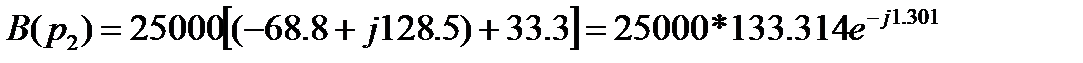
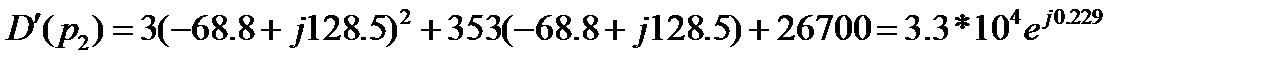
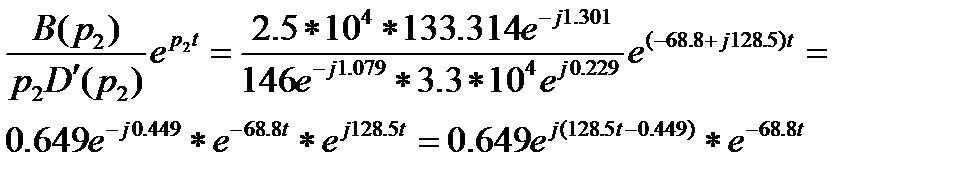 (3)

При 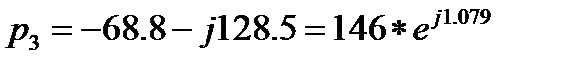 получим:   

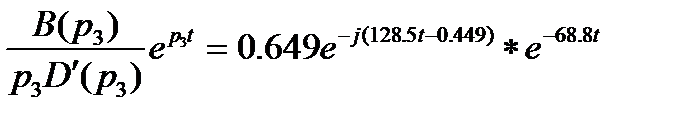(4)

Выражение (4) записано без расчета, непосредственно по вид

выражения (3), так как корн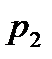и  и 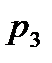 сопряженные, а коэффициенты в выражении (1) чисто вещественные. При этих условиях комплексные выражения (3), (4) заведомо являются сопряженными.

Если бы все корни характеристического уравнения были вещественными, то и расчет можно было бы закончить подстановкой этих выражений в формулу (1).

В данном случае выражения (3), (4) являются комплексными, поэтому их следует преобразовать. Применяя к сумме сопряженных выражений (3), (4)

формулу Эйлера:

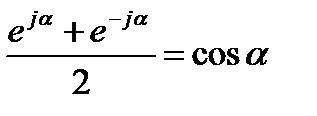
получим:

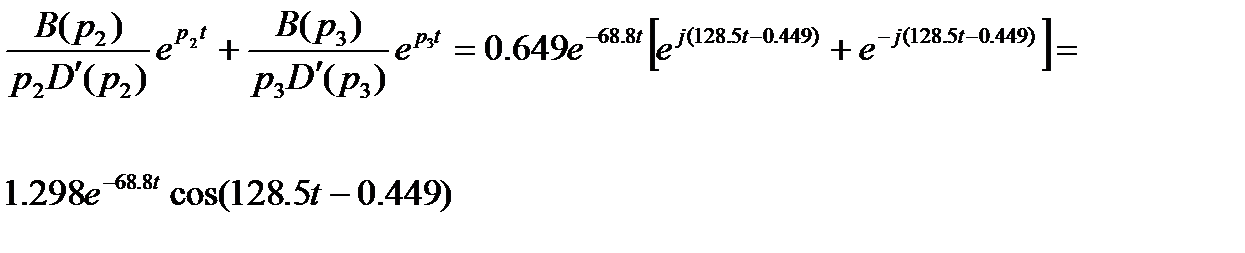
    Окончательный вид выходной величины:

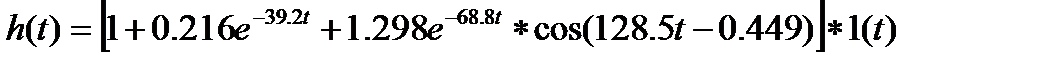
Для выполнения задания необходимо использовать различные формы представления комплексных чисел:

,

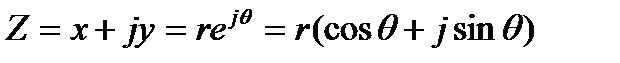 где: , .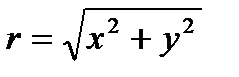

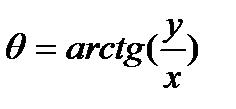Правила выполнения сложения и умножения комплексных чисел:

 

 

        

 

           

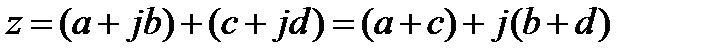
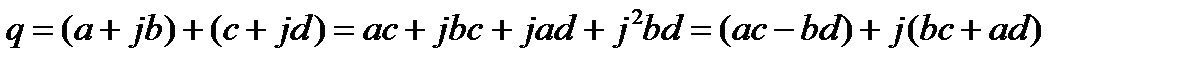
Звенья описываются уравнением вида:

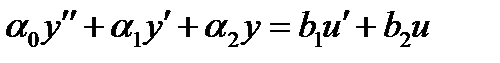
коэффициенты которого приведены в таблицах:

№
                             
№
                             

 

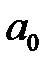
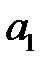
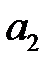
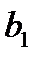
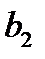
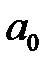
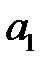
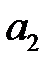
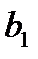
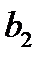
Программа работы

 

 



  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.