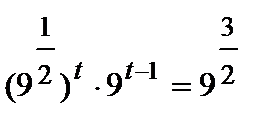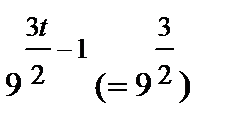- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Математика 10 сынып

| “Назарбаев Зияткерлік мектептері” ДББҰ Кембридж Халық аралық емтихандық кең есі |
Математика 10 сынып
1-емтиханжұ мысы
Баллқ оюсхемасының ү лгісі
Максималбалл: 80
| Балл қ ою кестесінің аннотациялвры жә не қ ысқ артулары Mә діс қ олданғ аны ү шін Aдұ рыс жауап (дә лдік) ү шін Bтә уелсіз балл ftқ ате есептеуден шығ ады depтә уелді |
| Сұ рақ | Жауап | Балл | Қ осымша нұ сқ аулар |
| 1(a) | 1, 2, 3, 6, 9, 12 | B2 [2] | B1 берің із егербірэлементіжеткіліксізнемесеқ атеболса (элементтерқ айталансаB1беругеболады) немесе егер кө рінсе (A = ) 3, 6, 9, 12 немесе (B =) 1, 2, 3, 6, 9 |
| 1(b) | B1 [1] | ||
| Барлығ ы[3] | |||
| 4x3 | B1 [1] | ||
| Барлығ ы[1] | |||
| 3(a) | 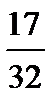 жә не жә не 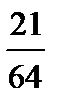
| B2 [2] | B1 берің ізбірдұ рысбө лшекү шін немесе бө лімдердің екідұ рысмә ніү шін немесе алымдардың екідұ рысмә ніү шін. |
| 3(b) | ‘Жоқ ’белгілейдіжә недұ рыстү сініктемебереді, мысалы,
· Тізбек жалғ асады 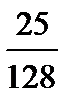 , ,  , , 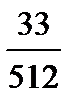 …
· Бө лімі 1024 болғ анда, алымы37 болады
· Бө лімі 512 болуы керек
· n-ші мү шесінің формуласы …
· Бө лімі 1024 болғ анда, алымы37 болады
· Бө лімі 512 болуы керек
· n-ші мү шесінің формуласы 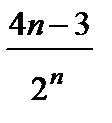 бойыншажә не10-дық оюарқ ылы. бойыншажә не10-дық оюарқ ылы.
| B1 [1] | Егердұ рыстү сініктемеберілсе, ‘Жоқ ’дегенкезкелгенанық жауаптық абылдаң ыз. |
| Барлығ ы[3] | |||
| 4(a) | 
| B1 [1] | Кезкелгендұ рыснұ сқ аманық абылдаң ыз. |
| 4(b) | Ромбжә недұ рыс негіздеме, мысалы, · OA = OD · OAжә неODрадиустар. | B2 [2] | B1 ромбнемесепараллелограмм атауы ү шін. |
| 4(c) | Іштейсызылғ антө ртбұ рыштың қ арама-қ арсыбұ рыштарының қ осындысы180°қ ұ райды. | B1 [1] | |
|
4(d) | Бұ рышODB = 40(°)
немесе
Бұ рышEOD = 40(°)
Бұ рышODE = 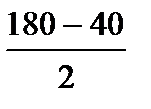 немесе 70(°)
30(°) немесе 70(°)
30(°)
| M1 M1 A1 | Суреттекө рсетілуімү мкін
M1 алдың ғ ыM1-деншығ ады. |
Альтернативтінұ сқ а:
Бұ рышCBD = 40(°)
Бұ рышACD = 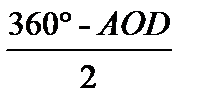 = 110 (°)
30(°) = 110 (°)
30(°)
| M1 M1 A1 [3] | ||
| Барлығ ы[7] | |||
| 5(a) | 
| B2 [2] | B1 берің ізграфиктедұ рыссалынғ анкоординаталардың біржиынтығ ыү шіннемесежұ мысынанкө рінсе |
| 5(b) | Осьтік симметрия (симметрия осі) x = 5 (немесеэквиваленттімә н) | B1 B1 [2] | |
| Барлығ ы[4] | |||
|
6(a) | (2x + a)(x + b), ондағ ы ab = − 30 немесе 2b + a = − 7 (2x+ 5)(x – 6) (x =) − 2, 5; 6 | M1 A1 A1ft | M1 балыберілгенкө бейткіштергежіктеуденшығ ады. |
Альтернативті нұ сқ а:
x = 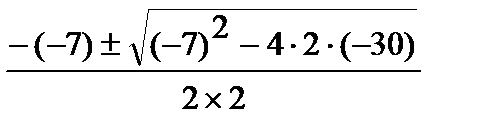 x =
x =  (x =) − 2, 5; 6
(x =) − 2, 5; 6
| M1 A1 A1 [3] | ||
| 6(b) | x × (2x – 5) немесе 2x2 – 5x немесе2 × (x – 3) немесе2x – 6 немесеx × (x – 2) немесеx2 – 2x немесе (x – 3) × (x – 2) немесеx2 – 2x – 3x + 6 немесе2 × (x – 2) немесе2x – 4 немесе (x – 2) × (2x – 5) немесе 2x2 – 5x – 4x + 10 немесе (x – 2) × (x – 2) немесеx2 – 2x – 2x + 4 2x2 – 7x + 6 эквивалентті ө рнек 36-ғ а тең естіріліп, дұ рыс есептелген жә не 2x2 – 7x – 30 = 0 ө рнегіне келтіреді | M1 A1 A1 [3] | Сә йкестіктө ртбұ рыштың ауданыү шіндұ рысалгебралық ө рнек. Ық шамдалмағ анболуымү мкін. Дұ рыстең деуденшығ ады. |
| 6(c) | (EF =) 2 ·ө зінің 6 – 5 немесе 7 немесе (CD =) ө зінің 6 – 3 немесе 3 немесе (AB =) ө зінің 6 – 2 4 (см) | M1 A1ft [2] | (a)бө лімінен шығ ады, ө зінің 3-тен ү лкен x ескере отырып. |
| Барлығ ы[8] | |||
| 7(a) | (1, 2) | B2 [2] | B1 ә р координата ү шін. |
| 7(b) | 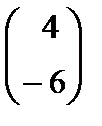
| B1 [1] | Немесе эквивалентті жазылу, мысалы 4i – 6j |
| 7(c) | 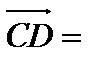  немесе немесе 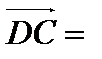 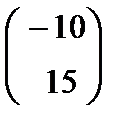 немесе
немесе 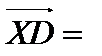  немесе немесе 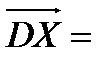 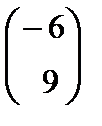
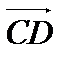 (немесе (немесе 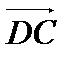 немесе немесе 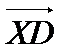 немесе немесе 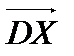 ) еселі ) еселі 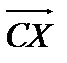 -ке, демек бір тү зу бойында жатыр. -ке, демек бір тү зу бойында жатыр.
| M1 A1 [2] | Немесеэквиваленттіжазылу Немесеекісә йкесвекторлардыэквиваленттітү рдесалыстыру |
| 7(d) | Дұ рыс қ ысқ артылмағ ан қ атынас
(мысалы, 4: 6 немесе 6: 9 немесе  : : 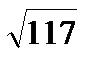 )
немесе )
немесе
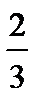 тү рі ү шін (немесе эквивалент)
немесе
3: 2 тү рі ү шін
2: 3 тү рі ү шін (немесе эквивалент)
немесе
3: 2 тү рі ү шін
2: 3
| M1 A1ft [2] | Ө зінің (b) жә не(c)-наншығ ады. |
| Барлығ ы[7] | |||
| 8(a) | 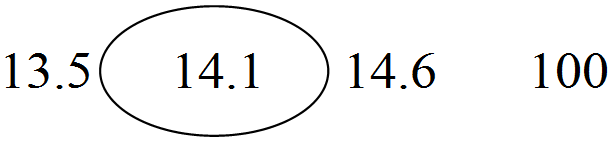
| B1 [1] | Кезкелген 14. 1дұ рыснұ сқ аманық абылдаң ыз |
| 8(b) | 1 мен 2 арасындағ ы кез келген иррационал сан | B1 [1] | Мысалдар
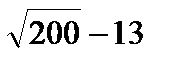 . .
|
| 8(c)(i) | Кө бейтіндісі рационал сан болатын кез келген екі иррационал сан | B1 [1] | Мысалдар
|
| 8(c)(ii) | Сә йкескелетінконтрмысалұ сынады (кө бейтіндісірационалсанболмайтынкезкелгенекіиррационалсан) | B1 [1] | Мысалдар · π × π (рационал емес) · √ 2 × √ 3 (рационал емес). |
| Барлығ ы[4] | |||
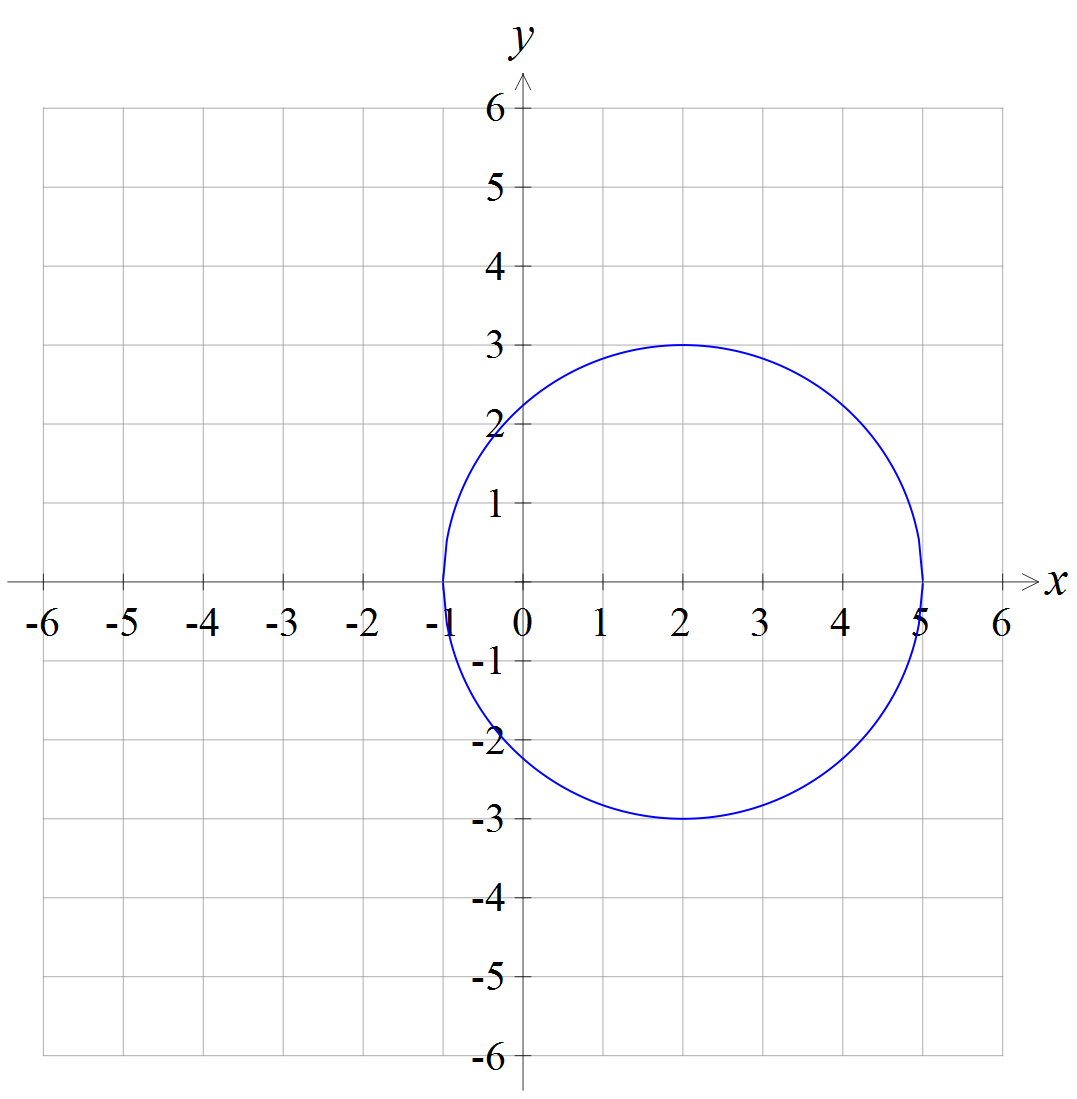
| B3 [3] | B1 шең берү шін B1 радиус = 3ү шін (суреттенкө рінуімү мкін) B1 центр = (2, 0) ү шін (суреттенкө рінуімү мкін) | |
| Барлығ ы[3] | |||
| 10(a)(i) | x> 3, x< –3 | B2 [2] | B1 x> 3 ү шін немесе x< − 3ү шін немесе 3 жә не –3 ү шін |
| 10(a)(ii) | (x + a)(x + b), ондағ ы ab = − 10 немесе a + b = − 3 (x− 5)(x + 2) − 2 < x< 5 | M1 A1 A1ft [3] | x2 – 3x – 10 (x2 – 3x емес) кө бейткіштерге жіктеу ә рекеті ү шін Бұ л балды дискриминант формуласын қ олданғ аны ү шін алуғ а болады от (x = ) 5, − 2 тү бірлерінен шығ уы мү мкін Ө зінің кө бейткіштерге жіктеуінен шығ ады |
| 10(b) | 3 < x< 5 | B1ft [1] | Ө зінің (a)бө ліміндегіжауаптарынаншығ ады(шешіміa< x< bнемесе a ≤ x ≤ bтү ріндегі бір интервал болса). |
| Барлығ ы[6] | |||
|
11(a) | 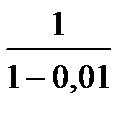 немесе немесе 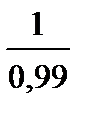
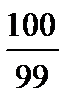 немесе немесе 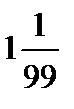
| M1 A1 | |
Альтернативтінұ сқ а:
S = 1, 010101… жә не 100S = 101, 010101…
мынағ анкелтіретін: 99S = 100
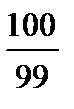 немесе немесе 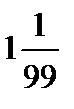
| M1 A1 [2] | ||
|
11(b) | 0. 27 · ө зінің 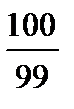 Дұ рыс,
Дұ рыс, 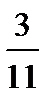 -ке келтіретін шешім -ке келтіретін шешім
| M1 A1 | |
Альтернативтінұ сқ а:
 немесеэквивалент
Дұ рыс, немесеэквивалент
Дұ рыс, 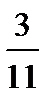 -ке келтіретін шешім -ке келтіретін шешім
| M1 A1 | Дұ рыс емес шешім кө рінбейді. | |
| Альтернативтінұ сқ а2: 30| 11___ 22 | 0, 27 80 0. 272(…. ) дейінтолық бө лінген, аргументтенкейінкө пнү ктеқ ойылғ ан | M1 A1 | 3-ті11-гебө луә дісіү шін0. 27(…). -гедейін 8 қ алдығ ы кө рінуі керек | |
Альтернативті нұ сқ а3:
x = 0. 2727… жә не 100x = 27. 27… жә не 99x = 27
Дұ рыс, 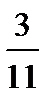 -ке келтіретін шешім -ке келтіретін шешім
| M1 A1 [2] | ||
| Барлығ ы[4] | |||
| 12(a) |
| B1 [1] | |||
| 12(b) | 52 + 82 – 2 · 5 · 8 ·cos(60)
89 – 40
(AC2 =) 49 немесе (AC =) 7
92 – их 49 немесе 92 – (их 7)2немесе 32
| M1 M1 A1ft M1 A1 [5] | Косинустартеоремасынадұ рысқ ойылғ ан Келесідұ рысамалретінбағ алауә рекеті. Ө зінің (a)бө лімінен шығ ады. | ||
| Барлығ ы[6] | |||||
|
13(a) | 

| M1 A1 [2] |
| ||
|
13(b) | Теріс таң балы дә режелермен амал, мысалы  Немесе
4 дә режелі тү бірмен амалдар, мысалы,
Немесе
4 дә режелі тү бірмен амалдар, мысалы, 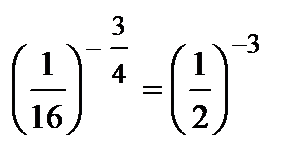 немесе немесе 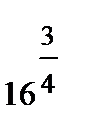 =23 =23
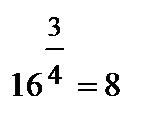 болатынын ұ йғ аратын шешім
0, 5 немесе эквивалент болатынын ұ йғ аратын шешім
0, 5 немесе эквивалент
| M1 A1 A1 [3] |
| ||
| Барлығ ы[5] | |||||
(c =) 2
(a =) 3
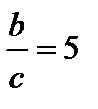 немесе эквивалент
(b =) 10 немесе эквивалент
(b =) 10
| B1 B1 M1 A1ft [4] | Ө зінің c-нан шығ ады. | ||
| Барлығ ы[4] | ||||
|
15(a) | 27 = 33немесе 9 = 32
(t= ) | M1 M1 M1 A1 | Ә рбір мү шесі бір санның дә режесімен ө рнектелген дұ рыс тең деу. Сол жағ ы дә режнің қ асиеттері кө мегімен ық шамдалғ ан (оң жағ ына мә н аудармаң ыз). | |
| Альтернативті нұ сқ а1: 3 =
(t= ) | M1 M1 M1 A1 | Ә рбір мү шесі бір санның дә режесімен ө рнектелген дұ рыс тең деу. Сол жағ ы дә режнің қ асиеттері кө мегімен ық шамдалғ ан (оң жағ ына мә н аудармаң ыз). | ||
Альтернативті нұ сқ а2:
3 = 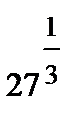 or 9 = or 9 = 

 (t= )
(t= ) 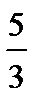
| M1 M1 M1 A1 [4] | Ә рбір мү шесі бір санның дә режесімен ө рнектелген дұ рыс тең деу. Сол жағ ы дә режнің қ асиеттері кө мегімен ық шамдалғ ан (оң жағ ына мә н аудармаң ыз). | |
|
15(b) |  (= 1) or equivalent (= 1) or equivalent
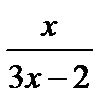 = 3
x = 9x – 6
(x = ) = 3
x = 9x – 6
(x = ) 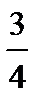
| M1 M1 M1 A1 | logқ асиеттеріндұ рысқ олдану. log3(…. ) = 1тү ріндегіө рнектендұ рысшығ ару Дұ рыссызық тық тең деу. Эквивалентбө лшектінемесеондық бө лшектіқ абылдаң ыз. |
Альтернативтінұ сқ а:
log3x = log3(3x – 2) + log33
log3x = log3(3(3x – 2))
x = 9x – 6
(x= ) 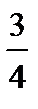
| M1 M1 M1 A1 [4] | logқ асиеттеріндұ рысқ олдану. Дұ рыссызық тық тең деу. Эквивалентбө лшектінемесеондық бө лшектіқ абылдаң ыз.. | |
| Барлығ ы[8] | |||
| 16(a) | 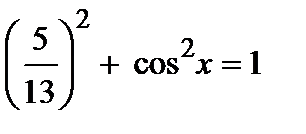
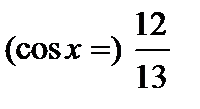


| M1 A1 M1 A1 [4] |
 қ олдану
Альтернатива: 5, 12, 13 ү шбұ рыш бейнеленген. қ олдану
Альтернатива: 5, 12, 13 ү шбұ рыш бейнеленген.
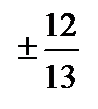 емес емес
|
| 16(b) |  немесе sin(34)
(y =) 17(°)
(y =) 73(°) немесе sin(34)
(y =) 17(°)
(y =) 73(°)
| M1 A1 A1ft [3] | 90 –ө зінің 17. |
| Барлығ ы [7] | |||
ТАЗА БЕТ
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
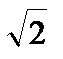
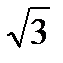
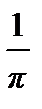 жә не π
жә не π  немесе 0. 5
немесе 0. 5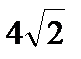 немесеk = 4
немесеk = 4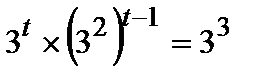
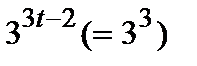
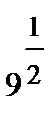 немеес 27 =
немеес 27 =