Разбор заданий тренировочного модуля.

26. 02. 21.

Тема: Алгебраические дроби и их свойства. Приведение алгебраических дробей к общему знаменателю

Перечень рассматриваемых вопросов:

· Алгебраическая дробь.

· Свойства алгебраических дробей.

Задание: запишите в тетради число и тему урока. Прочитайте текст и примеры. Запишите в тетрадь теоретический материал и примеры из текста вместе с объяснениями.

Теоретический материал для самостоятельного изучения.

Алгебраической дробью называют выражение 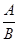- частное многочлена А и ненулевого многочлена В – (на 0 делить нельзя).

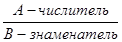
Например, 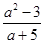- алгебраическая дробь.

а² – 3 – числитель дроби

а+5 – ее знаменатель

Свойства алгебраических дробей:

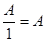
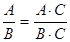- основное свойство алгебраической дроби

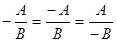
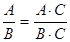- это основное свойство алгебраической дроби, но и приведение дроби к новому знаменателю В∙ С

Знание свойств алгебраических дробей поможет в дальнейшем в упрощении выражений, сокращении дробей, нахождении нового знаменателя и других задач.

Домножили числитель и знаменатель дроби на 5х
В знаменателе дроби вынесли за скобку 3 и получили одинаковый многочлен в числителе и знаменателе дроби (х+3) и теперь на него сокращаем и получаем .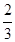

Итак: свойства алгебраической дроби или просто дроби

Разбор заданий тренировочного модуля.

№1. Тип задания: сократим дробь:

Разложим числитель дроби на множители, используя формулу разности квадратов, а в знаменателе разложим многочлен на множители способом группировки.

Запись в тетради: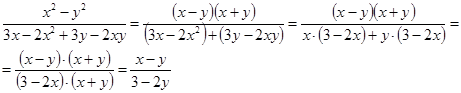

№2. Тип задания: сокращение дробей.

Сократим дробь и найдем условие, при котором нельзя найти значение выражения:

Запись в тетради: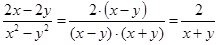

Значение дроби нельзя вычислить, если ее знаменатель равен 0 (на ноль делить нельзя).