Хелпикс

Главная

Контакты

Случайная статья



Решение задач.

⇐ ПредыдущаяСтр 2 из 2


Решение задач.

Пример 1:

Отрезки АС и ВD точкой их пересечения О делятся пополам. Докажите, что .

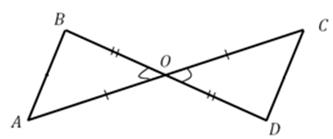Дано: АО=ОС, ВО=ОD.

                                  Доказать: ∆ АВО = ∆ СDО

 

 

                                    Доказательство.

1. АО=ОС – по условию.

2. ВО=ОD – по условию.

3. < АОВ = < СОD – как вертикальные.

Значит, ∆ АВО = ∆ СDО по первому признаку.

Пример 2:

Отрезки АС и BD точкой пересечения делятся пополам. Докажите, что .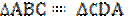

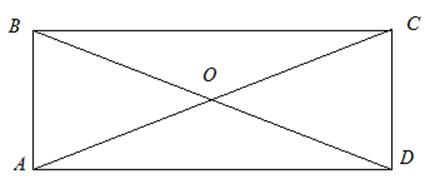 Дано: АО=ОС, ВО=ОD.

                                                                    Доказать: ∆ АВС = ∆ СDА

 

                                                Доказательство.

1.            АО=ОС – по условию.

2. ВО=ОD – по условию.

3. < АОВ = < СОD – как вертикальные.

Значит, ∆ АВО = ∆ СDО по первому признаку.

Теперь рассмотрим треугольники АВС и СDА.

1. АС – общая сторона.

Из равенства треугольников АВО и СDО следует:

2. АВ=СD.

3. ∠ OAB = ∠ OCD.

Значит, ∆ АВС = ∆ СDА по первому признаку.

 

Домашнее задание. Перепишите в тетрадь классную работу. Изучите п. 14, 15 учебника. Решите задачи: № 91, 93, 95, 99.


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.