Тема. Степень с натуральным показателем

Стр 1 из 2Следующая ⇒

Тема. Степень с натуральным показателем

5-А класс

03. 11. 2021

Ход урока.

Перечень вопросов, рассматриваемых в теме:

- понятие степени с натуральным показателем;

- вычисление квадрата числа;

- вычисление куба числа.

Теоретический материал для самостоятельного изучения

Нам известно, что сумму нескольких одинаковых слагаемых принято записывать короче – в виде произведения:

4 + 4 + 4 + 4 + 4 = 4 ∙ 5

Произведение одинаковых чисел также можно записать короче:

4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4⁵

Это произведение можно записать короче, полученный результат называют степенью. Читается так: «четыре в пятой степени».

Запись 4³ (четыре в степени три) означает 4 ∙ 4 ∙ 4. При этом число 4 называют основанием степени, а число 3 – показателем степени. Число три показывает, сколько раз нужно взять множителем основание степени – число 4: 4³ = 4 ∙ 4 ∙ 4 = 64.

Степенью числа а с натуральным показателем n (n > 1) называют произведение n натуральных множителей, каждый из которых равен а:

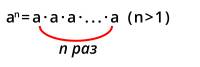
Рассмотрим несколько примеров. Вычислим 2⁵, 2 в качестве множителя повторяется 5 раз, значит: 2⁵ = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32.

Теперь вычислим 3⁷. 3 в качестве множителя повторяется 7 раз, значит: 3⁷= 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 3 = 2187.

Таким образом, можно вычислить любую степень числа с натуральным показателем, большим единицы. Стоит запомнить, что любое число в первой степени будет ровняться ему самому, т. е. a¹= a.

Вторую степень числа называют квадратом числа. Запись 4² читают «четыре в квадрате». Третью степень числа называют кубом числа. Запись 4³ читают «четыре в кубе».

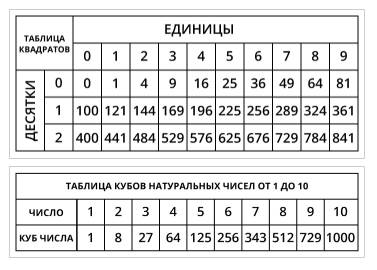
Обратите внимание на таблицы квадратов и кубов натуральных чисел. Со временем вы их запомните.

12 Следующая ⇒