I метод вычислений

Практическая работа

«Моделирование второго закона Кеплера»

Алгоритм выполнения:

1. Строим эллипсы (см. видео).

2. Отмечаем точки D, K, O, S, A, B.

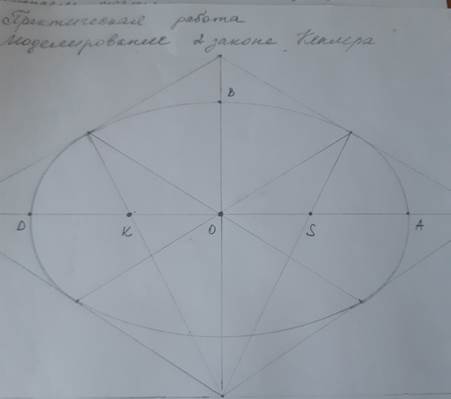
I метод вычислений

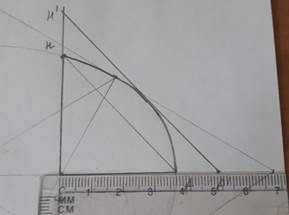
3. Проводим из точки S перпендикуляр, и точку пересечения с эллипсом обозначим H. Получаем сектор 1, площадь которого мы будем находить.

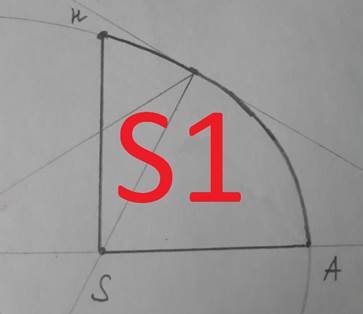
4. Соединим точки H и A, получим треугольник HSA, его площадь меньше искомой площади сектора 1.

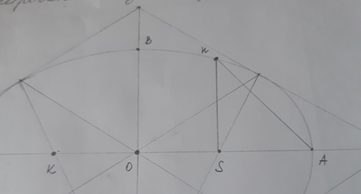
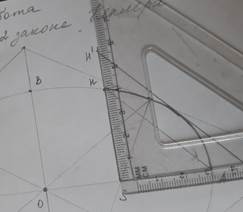
5. С помощью параллельного переноса прямой HA построим касательную к дуге HA. Обозначим точки пересечения касательной с вертикальной и горизонтальной прямыми H` и А` соответственно. Соединим точки H` и А`, получим треугольник H`SA`, его площадь больше искомой площади сектора 1.

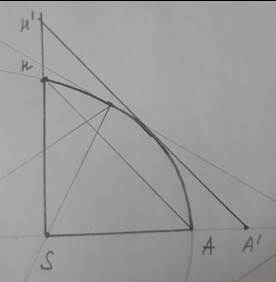
6. Найдем площади малого и большого треугольников, для этого измерим SH, SA, SH`, SA`.

7. Формулы для вычисления площадей:

S_HSA=1/2*SH*SA

S_H`SA`=1/2*SH^`*SA^`

8. Так как S треугольника HSA меньше искомой, а S треугольника H`SA`, то найдем среднюю площадь S1

S₁=(S_HSA+ S_H`SA`)/2

9. Найдем вторую площадь S2 равную площади S1, она представляет сектор 2. Сектор 2 мы не можем изобразить, тк не знаем на каком расстоянии точка С находится от точки D

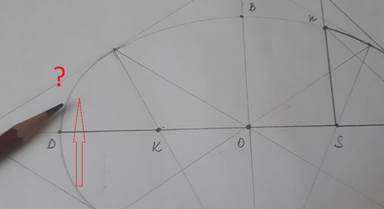
10. Так как дуга в точке D имеет не очень крутой изгиб, будем считать, что искомая площадь равно площади треугольника CSD, эта площадь по 2 закону Кеплера равна S1. И находится по формуле:

S_HSA=S1=1/2*SD*CD

11. Использую предыдущие расчеты мы нашли числовое значение S1, измерим SD

12. Найдем CD.

CD=2*S1/SD

13. Отметим на эллипсе значение равное CD и обозначим точку С, соединим ее с точкой S. Получим сектор CSD.

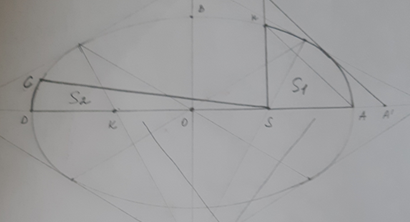
14. Площадь сектора HSA равна площади CSD.

12 Следующая ⇒