Законы И.Кеплера

Небесная механика

Законы Кеплера. Длительное время считалось, что движение планет может происходить только по окружности. Однако многолетние наблюдения за планетами заставили усомниться в такой форме планетных орбит. Опираясь на результаты наблюдений выдающегося датского астронома Тихо Браге, Иоганн Кеплер, немецкий математик и астроном (рис. 2. 35), доказал, что траектории движения планет вокруг Солнца — эллипсы, и стал первооткрывателем законов движения небесных тел.

Рис. 2. 35. Иоганн Кеплер (1571—1630)

Первый и второй законы движения небесных тел И. Кеплер опубликовал в 1609 г. в книге «Новая астрономия».

Первый закон Кеплера: все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце (рис. 2. 36). Фокусы — это две точки, сумма расстояний от которых до любой точки эллипса является постоянной. На рис. 2. 36 показана эллиптическая орбита планеты. Солнце находится в одном из фокусов эллипса (F₁ или F₂). Ближайшая к Солнцу точка траектории называется перигелием, точка, наиболее удаленная от Солнца, — афелием. Прямая, соединяющая афелий и перигелий, — большая ось эллипса. Половина большой оси — среднее расстояние планеты от Солнца. Текущее положение планеты, движущейся по своей орбите вокруг Солнца, отмечено точкой М.

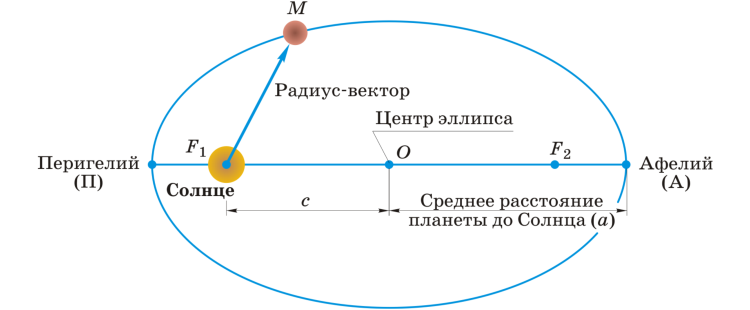Рис. 2. 36. Иллюстрация первого закона Кеплера

По эллиптическим орбитам движутся не только планеты, но и их естественные и искусственные спутники. В реальности орбиты планет нашей Солнечной системы не так вытянуты, как показано на рис. 2. 36, и близки к круговым. Перигелий Земли составляет 147098291 км, афелий — 152098233 км. Различие в 5 млн км является очень небольшим по космическим масштабам. В ближайшей к Солнцу точке своей орбиты Земля бывает зимой, а в наиболее удаленной — летом: Земля проходит перигелий 2—5 января, а афелий — между 3 и 7 июля. При современных параметрах земной орбиты влияние на климат наклона оси вращения планеты более значимо, чем расстояние Земли от Солнца. В Северном полушарии Земли наступает лето, когда Северный полюс Земли освещается Солнцем, а Южный полюс планеты располагается в ее тени.

Нарисовать эллипс самим очень легко. Воткните две кнопки, между ними привяжите нитку с большей длиной, чем расстояние между кнопками. Затем, натягивая карандашом нить, начертите эллипс с фокусами в точках, где находятся кнопки. Поместив в один из фокусов Солнце, определите положение перигелия, афелия, большую полуось гипотетической планеты. Измените расстояние между кнопками и посмотрите, как изменится форма эллипса.

Второй закон Кеплера: радиус-вектор планеты описывает равные площади за равные промежутки времени (рис. 2. 37). (Под радиус-вектором понимается вектор, проведенный от Солнца к планете. ) Это означает, что чем дальше планета от Солнца, тем медленнее она движется. Как показано на рис. 2. 37, площади S₁ и S₂ одинаковы, а расстояния, пройденные планетой по своей орбите за одинаковые промежутки времени, различны. Из этого следует, что вблизи перигелия скорость движения планеты должна быть больше, чем в афелии. Для Земли в перигелии орбитальная скорость составляет 30, 2 км/с, а в афелии — 29, 2 км/с.

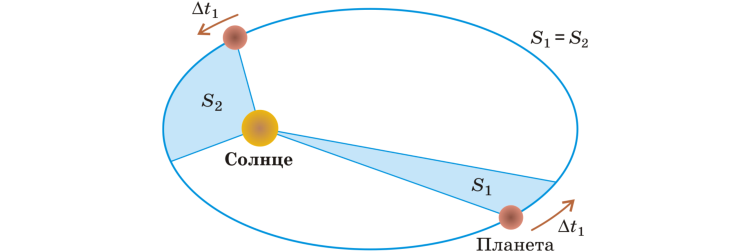Рис. 2. 37. Иллюстрация второго закона Кеплера

Третий закон Кеплера, открытый в 1619 г., звучит следующим образом: квадраты периодов обращения планет относятся как кубы больших полуосей их орбит:

где Т₁ и Т₂ — периоды обращения планет; a₁ и a₂ — большие полуоси их орбит.

Как и первые два закона, третий закон Кеплера применяется для описания движения не только планет, но и их естественных и искусственных спутников. Благодаря ему можно было легко вычислить относительные расстояния планет от Солнца (в астрономических единицах), зная их периоды обращения вокруг Солнца. Законы Кеплера, полученные на основе астрономических наблюдений, явились важнейшим этапом в понимании движения планет.

После смерти И. Кеплера осталось одно изношенное платье, две рубашки, несколько медных монет и… 57 вычислительных таблиц, 27 напечатанных научных трудов, огромное рукописное наследие, собранное позже в 22 книгах. Однако самое главное наследство великого ученого — три закона движения планет. В 1774 г. Петербургская академия наук приобрела бó льшую часть архива (18 томов), он и сейчас хранится в Санкт-Петербургском филиале архива РАН.

Теоретическое обоснование этих законов предложил Исаак Ньютон (рис. 2. 38), открывший в 1682 г. закон всемирного тяготения: все тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними:

где G — гравитационная постоянная, G = 6, 67 · 10^{− 11}(Н · м²)/кг²; M и m — массы Солнца и планеты соответственно; R — расстояние между ними.

Рис. 2. 38. Исаак Ньютон (1643—1722)

Ньютон первый предположил, что гравитационные силы действуют между любыми телами Вселенной и определяют движение планет Солнечной системы и их спутников. Законы Кеплера Ньютон вывел из закона всемирного тяготения. Он доказал, что под действием силы тяготения одно небесное тело может двигаться по отношению к другому по различным траекториям: окружности, эллипсу, параболе и гиперболе.

Ньютон установил, что третий закон Кеплера не совсем точен — в действительности в него входят и массы Солнца и планет:

где Т₁ и Т₂ — сидерические периоды планет; М₀ — масса Солнца; m₁ и m₂ — массы планет; a₁ и a₂ — полуоси орбит планет.

Поскольку движение и масса оказались связаны, эту комбинацию третьего закона Кеплера и закона всемирного тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды. Использование третьего обобщенного закона Кеплера также позволяет определить массы двойных звезд по элементам их орбит.

Открытие Нептуна и Плутона. Движение планет по строго эллиптическим орбитам происходит только под действием притяжения одного тела — Солнца. Однако любая планета испытывает притяжение со стороны других планет, спутников планет, любых других тел, обладающих массой, поэтому ее движение подчиняется законам Кеплера неточно. В результате этого возникают отклонения от эллиптической траектории, которые называются возмущениями.

Впервые еще в XIX в. расчет возмущений планет позволил открыть новые неизвестные тела. В 1781 г. немецкий астроном Вильям Гершель, который был к тому же и композитором, открыл седьмую планету, названную впоследствии Ураном. Примерно через полвека выяснилось, что в движении планеты наблюдаются отклонения от кеплеровской орбиты, не согласующиеся с расчетными даже при учете возмущений со стороны всех известных планет. На основе математических расчетов французского математика Урбена Леверье было вычислено положение новой планеты в пространстве, и в 1846 г. немецкий астроном Иоганн Галле ее обнаружил. Неизвестную ранее планету назвали Нептун. В дальнейшем и в движении Урана и Нептуна были замечены возмущения, которые в 1930 г. увенчались открытием еще одного ранее неизвестного тела — карликовой планеты Плутон.

Из планет наибольшие возмущения в движении тел Солнечной системы вызывает Юпитер. При прохождении вблизи Юпитера астероидов и комет возникают заметные отклонения. Например, если ускорение кометы, вызванное притяжением Юпитера, будет направлено в ту сторону, в которую направлено ее ускорение к Солнцу, комета может развить такую большую скорость, что, двигаясь по гиперболе, навсегда уйдет из Солнечной системы. В противоположном случае притяжение Юпитера сдерживает комету, ее орбита меняется, а период обращения резко уменьшается.

В настоящее время возмущения учитываются при вычислении положения планет, их спутников и других тел Солнечной системы, а также для расчета траекторий автоматических межпланетных станций.

Резюме. Законы небесной механики — три закона Кеплера и закон всемирного тяготения Ньютона — полностью объясняют движения планет, их естественных и искусственных спутников, других космических тел. Открытие Нептуна и Плутона «на кончике пера» доказало справедливость гелиоцентрической системы и законов небесной механики.

Контрольные вопросы

В чем состоят законы Кеплера?
Когда планета находится ближе к Солнцу: в афелии или перигелии?
В какой точке орбиты скорость планеты больше?
Какое уточнение в третий закон Кеплера внес Ньютон?
Как формулируется закон всемирного тяготения?
Что называется возмущениями?
Почему наибольшие возмущения в движении тел Солнечной системы вызывает Юпитер?
Какие тела Солнечной системы были открыты благодаря их влиянию на орбиты других планет?

Задание для самостоятельной работы

Заполните таблицу.

Законы И. Кеплера
Формулировка закона	Графическая интерпретация
Первый закон:
Второй закон:
Третий закон:
Границы применимости:
Значение законов:

Темы докладов

Научная деятельность Тихо Браге.
Значение закона всемирного тяготения для открытия планет.
Законы небесной механики и научная картина мира.