
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение синуса и косинуса. Если точка на числовой окружности соответствует числу , то абсциссу точки называют косинусом числа , а ординату точки называют синусом числа .. Задача 1
Синус и косинус.
На этом уроке мы повторим сведения о числовой окружности и ее важное свойство. Дадим определение синуса и косинуса на базе координат числовой окружности. Далее решим типовые прямые и обратные задачи с синусом и косинусом числа.
Определение синуса и косинуса
Поместим числовую окружность (окружность с радиусом, равным 1) в координатную плоскость (см. Рис. 1). Точки 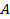 ,
, 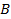 ,
, 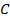 ,
, 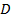 – это точки пересечения числовой окружности с осями координат.
– это точки пересечения числовой окружности с осями координат.
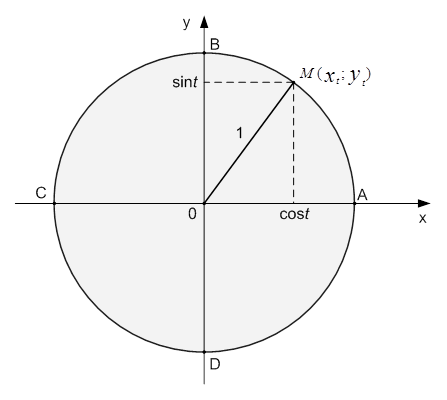
Рис. 1. Числовая окружность в координатной плоскости
Числу  соответствует единственная точка
соответствует единственная точка 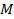 с координатами
с координатами 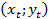 . Первая координата – это косинус числа
. Первая координата – это косинус числа  , вторая координата – это синус числа
, вторая координата – это синус числа  .
.
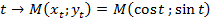
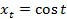
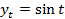
Если точка на числовой окружности соответствует числу, то абсциссу точки называют косинусом числа, а ординату точки называют синусом числа.
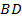 – это линия синусов. Синус любого числа
– это линия синусов. Синус любого числа  лежит в пределах от
лежит в пределах от 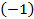 до
до 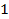 .
.
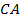 – это линия косинусов. Косинус любого числа
– это линия косинусов. Косинус любого числа  лежит в пределах от
лежит в пределах от 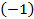 до
до 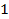 .
.
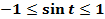
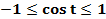
Задача 1
Дано: 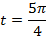 .
.
Найти: 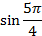 ;
; 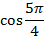 .
.
Решение
Решим данную задачу двумя способами:
1 способ (см. Рис. 2)
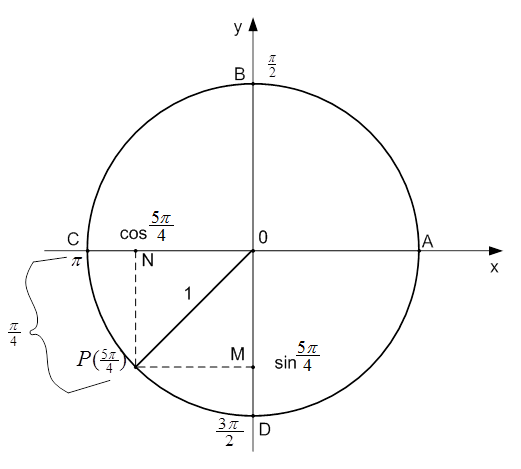
Рис. 2. Иллюстрация к задаче
1. Отметим на единичной окружности точку 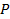 , которая соответствует заданному числу
, которая соответствует заданному числу 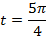 :
:
Число 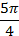 можно представить в виде
можно представить в виде 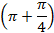 . Точка
. Точка 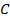 на числовой окружности соответствует числу
на числовой окружности соответствует числу 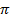 , следовательно, точка
, следовательно, точка 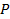 будет лежать на числовой окружности в третьем координатном углу.
будет лежать на числовой окружности в третьем координатном углу.
2. Опускаем перпендикуляры из точки 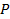 на оси координат:
на оси координат:
- точка 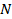 – это точка пересечения перпендикуляра с осью
– это точка пересечения перпендикуляра с осью 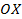 , координаты этой точки
, координаты этой точки 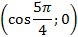 .
.
- точка 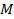 – это точка пересечения перпендикуляра с осью
– это точка пересечения перпендикуляра с осью 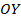 , координаты этой точки
, координаты этой точки 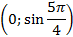 .
.
3. Рассмотрим 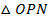 :
:
- гипотенуза 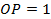 .
.
- угол 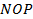 равен угловому измерению дуги
равен угловому измерению дуги 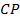 , то есть
, то есть  .
.
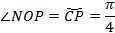
- катет 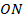 равен произведению гипотенузы на косинус прилежащего угла, то есть:
равен произведению гипотенузы на косинус прилежащего угла, то есть:
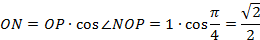
- этот прямоугольный треугольник является равнобедренным, так как один из его углов равен 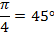 , следовательно:
, следовательно: 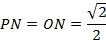
Так как 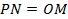 , то
, то 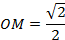 .
.
Значит, 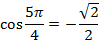 ,
, 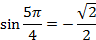 (в обоих случаях знак минус, так как точка
(в обоих случаях знак минус, так как точка 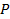 лежит на числовой окружности в третьем координатном углу, где значения координаты
лежит на числовой окружности в третьем координатном углу, где значения координаты 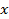 и
и 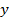 отрицательны).
отрицательны).
2 способ
Воспользуемся следующими свойствами:
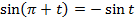
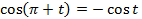
Согласно этим свойствам получаем:
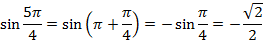
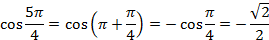
Ответ: 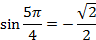 ;
; 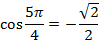 .
.
Задача 2
Решить уравнение:
1. 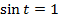
Решение
Синус числа – это ордината точки, находящейся на числовой окружности (см. Рис. 3). Поэтому чтобы определить, где 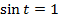 , нам надо найти, где на единичной окружности
, нам надо найти, где на единичной окружности 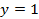 . Двигаясь вверх по оси
. Двигаясь вверх по оси 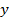 , попадаем в точку
, попадаем в точку 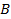 , которая соответствует числу
, которая соответствует числу  .
.
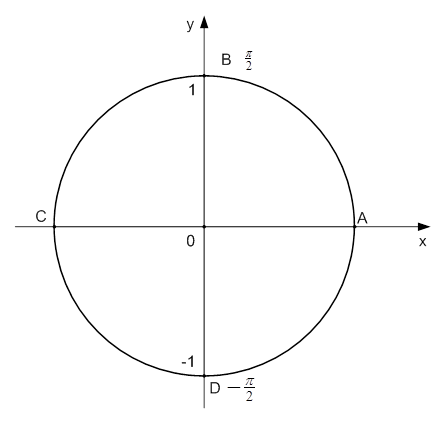
Рис. 3. Иллюстрация к задаче
Это только одна из точек, в которых синус равен 1. Через полный оборот окружности мы снова попадем в эту точку, через два, три и так далее – тоже. Чтобы учесть все точки, в которых 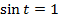 , необходимо к
, необходимо к 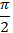 прибавить
прибавить 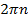 , где
, где 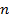 – целое число, то есть
– целое число, то есть  .
.
Ответ: 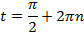 , где
, где 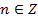 .
.
2. 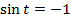
Решение
Отрезок 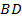 – это линия синусов (см. Рис. 3). При этом значение
– это линия синусов (см. Рис. 3). При этом значение 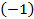 синус принимает в точке
синус принимает в точке 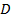 , которая соответствует числу
, которая соответствует числу 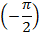 . Через полный оборот окружности мы снова попадем в эту точку, через два, три и так далее – тоже. Чтобы учесть все точки, в которых
. Через полный оборот окружности мы снова попадем в эту точку, через два, три и так далее – тоже. Чтобы учесть все точки, в которых 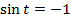 , необходимо к
, необходимо к 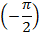 прибавить
прибавить 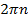 , где
, где 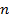 – целое число, то есть
– целое число, то есть  .
.
Ответ: 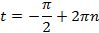 , где
, где 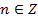 .
.
3. 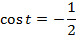
Решение
Отрезок 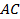 – это линия косинусов (см. Рис. 4). Обозначим на этой линии точку
– это линия косинусов (см. Рис. 4). Обозначим на этой линии точку 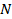 с координатами
с координатами 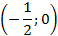 . Эта точка будет лежать посередине отрезка
. Эта точка будет лежать посередине отрезка 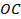 , так как
, так как 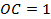 .
.
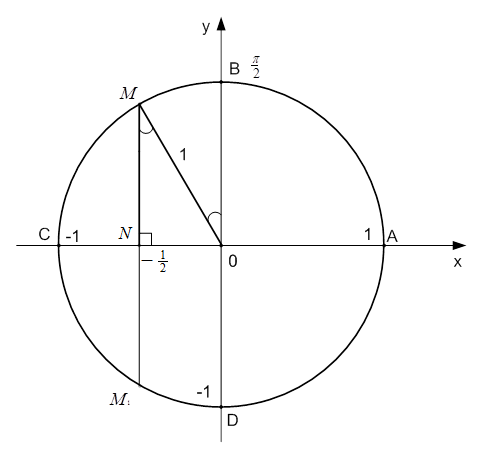
Рис. 4. Иллюстрация к задаче
Проведем через точку 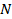 перпендикуляр к оси
перпендикуляр к оси 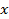 . Мы получили две точки на пересечении перпендикуляра и числовой окружности –
. Мы получили две точки на пересечении перпендикуляра и числовой окружности – 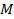 и
и 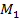 (только эти точки проектируются на линию косинусов в точку
(только эти точки проектируются на линию косинусов в точку 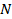 ).
).
Необходимо определить длину дуги 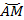 . Данная дуга состоит из дуги
. Данная дуга состоит из дуги 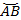 , длина которой равна
, длина которой равна  , и дуги
, и дуги  :
:
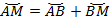
Для того чтобы определить длину дуги  , рассмотрим треугольник
, рассмотрим треугольник 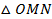 . Этот треугольник прямоугольный, катет
. Этот треугольник прямоугольный, катет 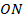 равен половине гипотенузы
равен половине гипотенузы 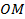 , следовательно, угол
, следовательно, угол 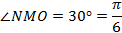 . Так как углы
. Так как углы 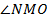 и
и 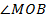 – это накрест лежащие углы, то
– это накрест лежащие углы, то 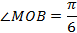 . Отсюда следует, что
. Отсюда следует, что 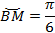 .
.
Таким образом:
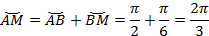
Следовательно, точке 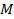 соответствуют числа
соответствуют числа 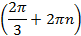 , где
, где 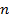 – целое число. Аналогично точке
– целое число. Аналогично точке 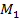 соответствуют числа
соответствуют числа 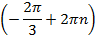 , где
, где 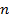 – целое число.
– целое число.
Ответ: 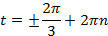 , где
, где 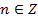 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|