Тема: Простейшие неравенства для косинуса

Уважаемый обучающийся, все работы выполняются в рабочих тетрадях по математике. Работа выполняется синей пастой.

Тема: Простейшие неравенства для косинуса

Цель: формирование умений обучающихся решать простейшие тригонометрические неравенства cos x> a; cos x < a.

1. Записать в тетрадь, зарисовать рисунки.

Неравенство cosx> a

1) При a≥ 1 неравенство cosx> a не имеет решений: x∈ ∅

2) При a< − 1 решением неравенства cosx> a является любое действительное число: x∈ R

3) При − 1< a< 1 решение неравенства cosx> a имеет вид: х∈ (− arccosa+2π n; arccosa+2π n), n∈ Z (см. рис)

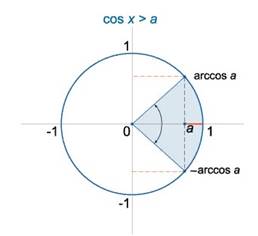
Неравенство cosx< a

1) При a> 1 неравенство cosx< a справедливо при любом действительном значении x: x∈ R

2) При a≤ − 1 неравенство cosx< a не имеет решений: x∈ ∅

3) При − 1< a< 1 решение неравенства cosx< a записывается в виде: x∈ (arccosa+2π n; 2π − arccosa+2π n)n∈ Z (см. рис. )

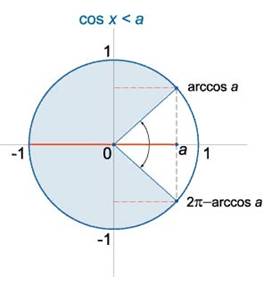
Решение неравенств cos x> a; cos x < a с помощью графика функции(ознакомиться)

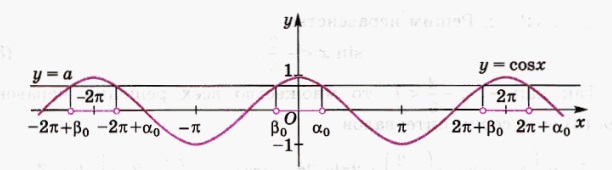
Рассмотрим графики функций у=cos x и у=а, |a|< 1. Из рисунка видим, что на промежутке длиной 2π (главный период) от β ₀до 2π +β ₀решениями неравенства cos x> a являются все хÎ (β ₀; α ₀), а решениями неравенства cos x < a являются хÎ (α ₀; 2π +β ₀), где α ₀=arccosa, β ₀= -α _0.

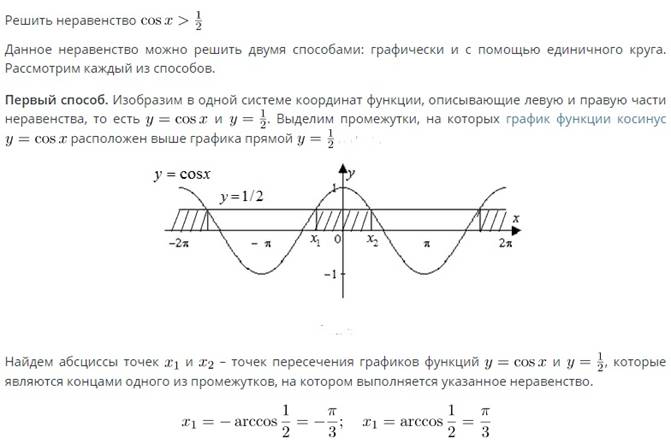
2. Рассмотрим решение неравенства.

Рассмотрим решение следующего неравенства несколькими способами.

3. Домашнее задание.

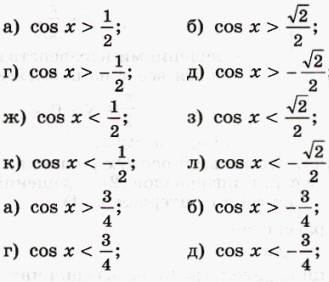№ 1

№ 2.

Выполненные задания присылать с указанием группы и фамилии

в вк или эл. почта: masha_fin@mail. ru