
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЗАДАНИЕ. Определенный интеграл.. Таблица интегралов. Простейшие свойства определенного интеграла
ЗАДАНИЕ
1. В тетради по математике записать тему занятия, свойства определенного интеграла, формулу Ньютона-Лейбница.
2. Разобрать решение и записать в тетрадь примеры 1, 2, 3, 4.
3. Выполнить задания для самопроверки, используя примеры 2, 3, 4.
Определенный интеграл.
Таблица интегралов
1. 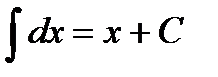 4.
4. 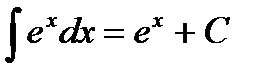 7.
7. 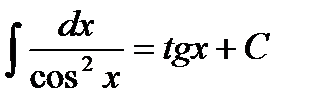
2. 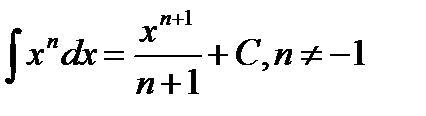 5.
5. 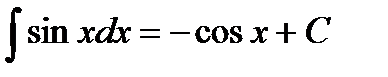 8.
8. 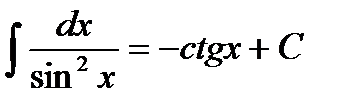
3. 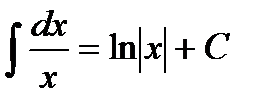 6.
6. 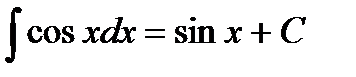
Пусть функция 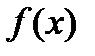 определена на отрезке
определена на отрезке 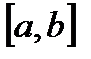 . Разобьем отрезок на n частей точками
. Разобьем отрезок на n частей точками 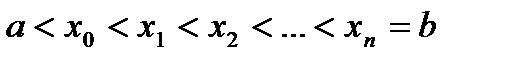 , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке 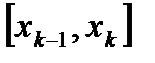 произвольную точку xk и обозначим через
произвольную точку xk и обозначим через 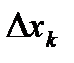 длину каждого такого отрезка.
длину каждого такого отрезка.
Интегральной суммой для функции 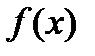 на отрезке
на отрезке 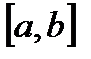 называется сумма вида
называется сумма вида
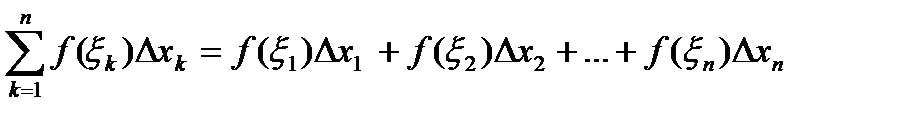 .
.
Определение. Определенным интегралом от функции 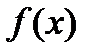 на отрезке
на отрезке 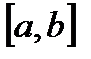 называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
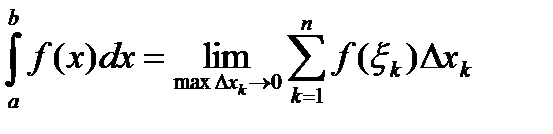 .
.
Для любой функции 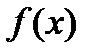 , непрерывной на отрезке
, непрерывной на отрезке 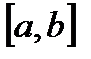 , всегда существует определенный интеграл
, всегда существует определенный интеграл 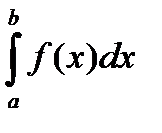 .
.
Простейшие свойства определенного интеграла
1) 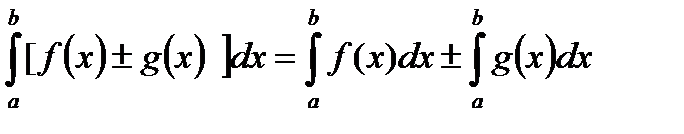 3)
3) 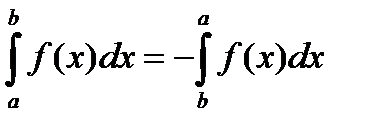
2) 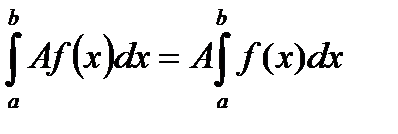 . 4)
. 4) 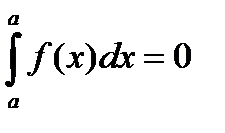
Формула Ньютона-Лейбница для вычисления определенного интеграла: 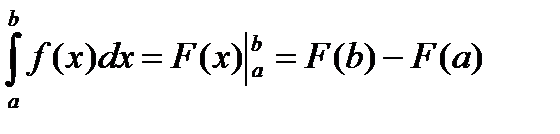
Вычислить определенный интеграл:
Пример 1. (формула 2) 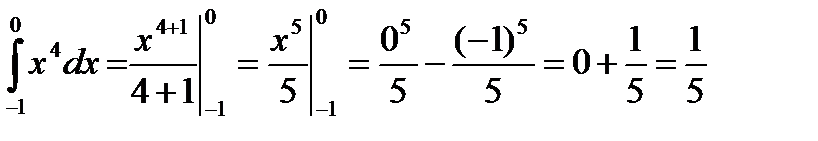
Пример 2. (правило 2 и формула 2) 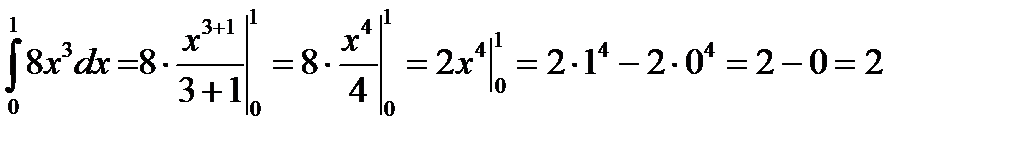
Пример 3. 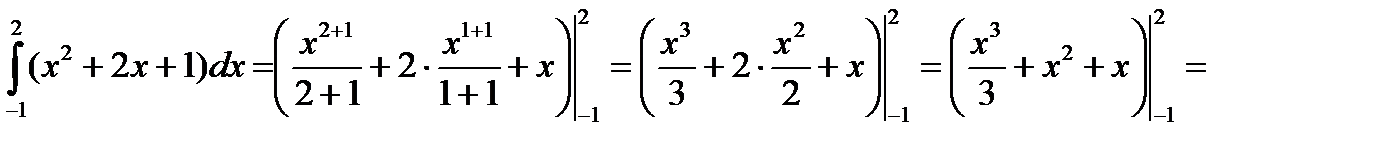
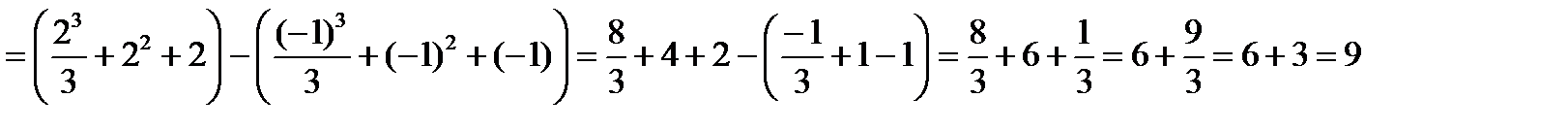
Пример 4. 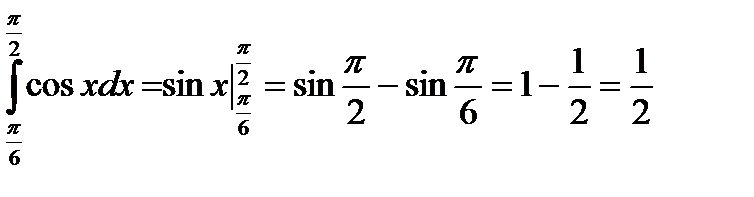
Задания для самопроверки:
№1. 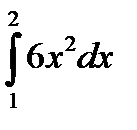 №2.
№2. 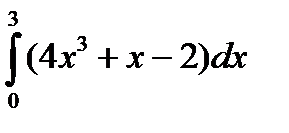 №3.
№3. 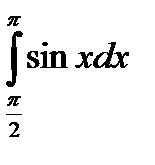
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|