Свойства решений однородной системы уравнений

1. Матрицы: основные понятия, транспонирование матрицы, линейные операции над матрицами, свойства линейных операций над матрицами.

2. Умножение матриц, свойства операции умножения.

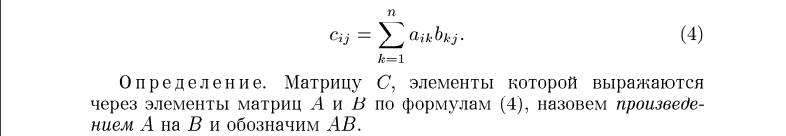
3. Детерминант: определение, влияние элементарных преобразований над строками

(столбцами) матрицы на ее детерминант

4. Теорема существования и единственности детерминанта, формула разложения

определителя по столбцу.

5. Детерминант 3-го порядка, детерминант транспонированной матрицы, детерминант

произведения матриц, свойство алгебраических дополнений.

Определителем или детерминантом третьего порядка, соответствующим матрице (1. 2), называется число равное

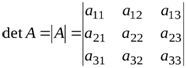
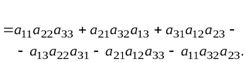
Структура этого выражения помогает понять наглядное правило Саррюса. Припишем к элементам определителя справа первый и второй столбцы определителя. Три произведения, соответствующие прямым, параллельным главной диагонали, надо взять со знаком плюс, а остальные три произведения, соответствующие прямым, параллельным побочной диагонали, надо взять его со знаком минус.

Определение 3. Минором 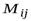элемента 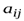определителя называется определитель, полученный из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен этот элемент, т. е. i – ой строки и j – го столбца.

Определение 4. Алгебраическим дополнением 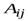элемента 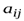определителя называется минор этого элемента, умноженный на 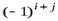, т. е. .

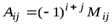Для вычисления алгебраических дополнений элементов определителей третьего порядка знаки легко запомнить по следующей схеме: .

Например: ;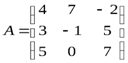

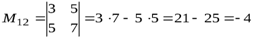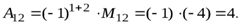
9⁰. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения.

Например: = .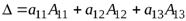

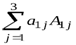10⁰. Сумма произведений элементов какого-нибудь столбца или строки определителя на алгебраические дополнения соответствующих элементов другого столбца или строки равна нулю.

Например: 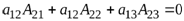или .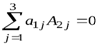

6. Системы линейных уравнений: основные понятия, элементарные преобразования системылинейных уравнений, теорема о равносильных системах.

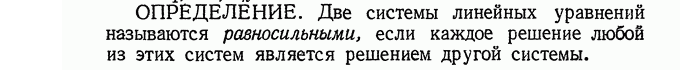
7. Трапециевидная форма матрицы, решение систем линейных уравнений методом Гаусса.

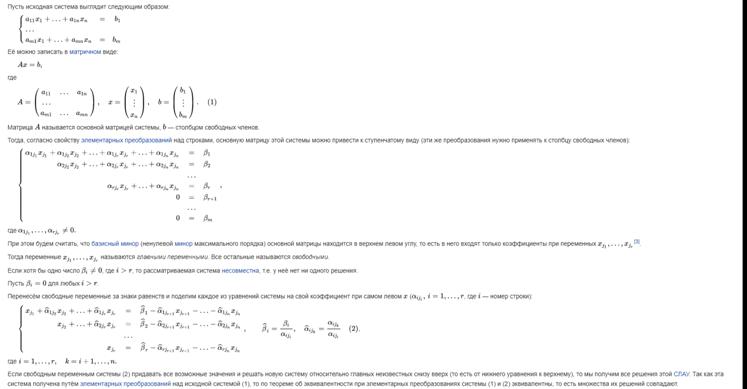
8. Теорема Крамера. Однородные системы линейных уравнений

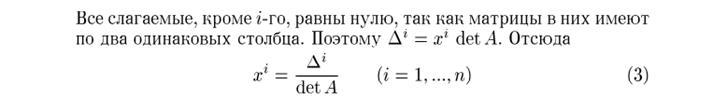
Свойства решений однородной системы уравнений

1. Если столбцы 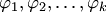— решения однородной системы уравнений, то любая их линейная комбинация 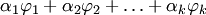также является решением однородной системы.

В самом деле, из равенств 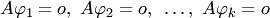следует, что

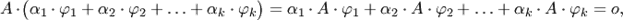т. е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеет линейно независимых решений.

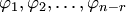Действительно, по формулам (5. 13) общего решения однородной системы найдем частных решений , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):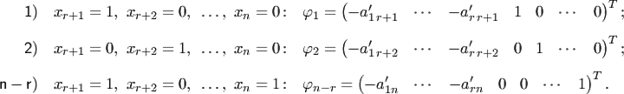

Получим решений

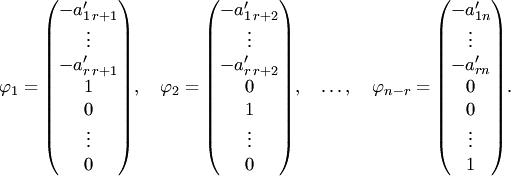которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних строках не равен нулю (он равен единице), т. е. является базисным. Поэтому ранг матрицы будет равен . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3. 4).

Любая совокупность линейно независимых решений 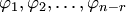однородной системы называется фундаментальной системой (совокупностью) решений.

Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества линейно независимых решений.