
- Р Р‡.МессенРТвЂВВВВжер
- ВКонтакте
- РћРТвЂВВВВнокласснРСвЂВВВВРєРСвЂВВВВ
- Telegram
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВРЎР‚
- LiveJournal
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
- визначник(детермінант) другого порядку
⇐ ПредыдущаяСтр 2 из 2
- визначник(детермінант) другого порядку
-визначник третього порядку
При обчисленні використовують формулу: 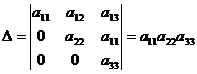
Алгебраїчне доповнення: 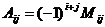
Визначник n-го порядку: 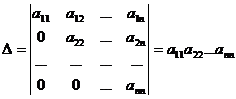
Матриця: 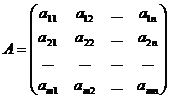 прямокутна таблиця, що складається з
прямокутна таблиця, що складається з 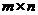 чисел
чисел 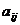
Одиничнаматриця: 
Вектор-стовпецьабо вектор-рядок: 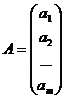 ,
, 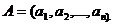
Квадратнаматрицявизначник, якої - не вироджена, а якщо визначник=0– вироджена.
Добуток матриць: 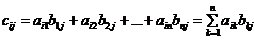
Обернена матриця: 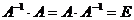

Матричні рівняння: 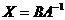 ;
; 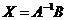 .
.
Ранг матриці – найвищий порядок відмінного від нуля мінора цієї матриці r(A), 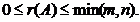
Cлар: система m рівнянь з n невідомими цього віглядуназ. системою лінійних алгебраїчних рівнянь.
Якщо, а принаймні один із визначників, то система – несумісна.
Якщо, і всі визначники дорівнюють нулю, то система – має безліч розв’язків.
Якщо, то СЛАР – має єдиний розв’язок, який знаходиться за формулами Крамера: .
Метод Гаусса: Якщо 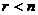 , то може бути два випадки:
, то може бути два випадки:
1) Хоча б одне з чисел не дорівнює нулю. Тоді система – несумісна;
2) Усі числа, …, рівні нулю. Тоді система– має безліч розв’язків, тобто невизначена.
Кронекера-Капеллі: r(A)=r( ) – СЛАР сумісна, r(A) - несумісна. r(A) =n – один розвязок. r(A) < n – безліч розв’язків. r(A) - несумісна.
Похідна: 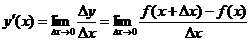
Рівняння дотичної до графіка ф-ї 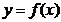 :
: 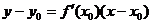
Рівняння нормалі: 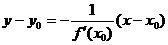
Основні правила диференціювання
1. 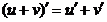 2.
2. 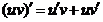
3. 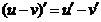 4.
4. 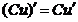
5. 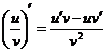
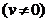 6.
6. 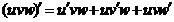
Похідна складеної функції: 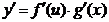

Похідна оберненої функції:  або
або 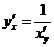
Похідна функції заданої параметрично: 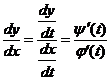 або
або 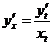
Похідна показниково-степеневої функції: 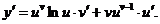
Похідна n-го порядку: 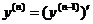 або
або 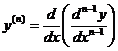
Формула Лейбніца: 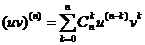
Похідні вищих порядків, задані параметрично:  ,
, 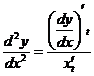 ,
, 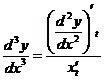
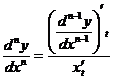
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|