
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
01.04.22.тема: «Преобразование целого выражения в многочлен»
01. 04. 22. тема: «Преобразование целого выражения в многочлен»
1. Разобрать решение примеров:
1. № 923.
Решение:
Преобразуем данное выражение:
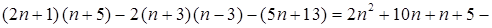
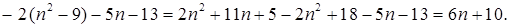
При любом целом п первое слагаемое полученной суммы делится на 6, а второе слагаемое не делится на 6. Значит, ни при каком целом п сумма 6п + 10 не делится на 6.
2. № 925.
Решение:
а) x (x + 2) (x – 2) – x (x2 – 8) = 16.
x (x2 – 4) – x3 + 8x = 16;
x3 – 4x – x3 + 8x = 16;
4х = 16;
х = 4.
Ответ: 4.
б) 2y (4y – 1) – 2 (3 – 2y)2 = 48.
8y2 – 2y – 2 (9 – 12y + 4y)2 = 48;
8y2 – 2y – 18 + 24y – 8y2 = 48;
22у = 66;
у = 3.
Ответ: 3.
3. № 927(а).
Решение:
а) Упростим данное выражение:
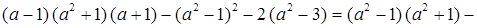
– a4 + 2a2 – 1 – 2a2 + 6 = a4 – 1 – a4 + 5 = 4.
Значит, значение выражения не зависит от а.
4*. № 999 (а).
Решение:
а) 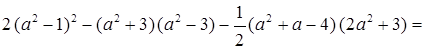
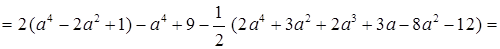
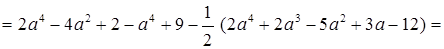 a4 – 4a2 + 11 –
a4 – 4a2 + 11 –
– a4 – a3 + 2, 5a2 – 1, 5a + 6 = –a3 – 1, 5a2 – 1, 5a + 17.
2. Решить
1. Преобразуйте в многочлен.
а) (c + 2) (c – 3) – (c + 1) (c + 3);
б) 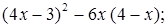
в) 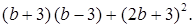
2. Найдите значение выражения
(3a + b)2 – (3a – b)2 при a = 3 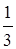 , b = –0, 3.
, b = –0, 3.
3. Упростите выражение 8 (5y + 3)2 + 9 (3y – 1)2.
Домашнее задание: № 926; № 928 (а); № 929 (а).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|