Второй замечательный предел

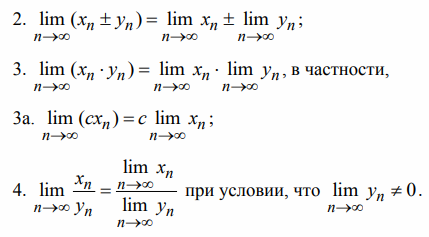
ПРЕДЕЛ ФУНКЦИИ.

Вычисление пределов

1) Подставляем значение к которому стремится переменная. Если в результате подставления получаем число, то получаем что предел не имеет неопределенностей и на этом решение данного предела закончено

( , )

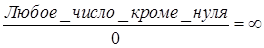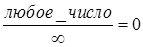2) Если получили какую либо неопределенность, то решаем предел в зависимости от вида неопределенности.

Для выяснения неопределенности можно предложить следующее: вынести за скобки в числителе и знаменателе высшую степень х каждого из них, а затем сократив степени х, снова пытаемся подставить и проверить не исчезла ли неопределенность.

Пример 1

Пример 2

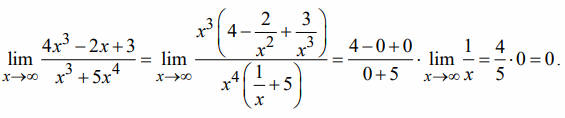
Пример 3

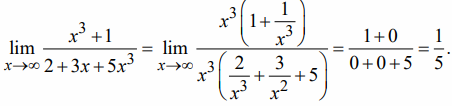
Если числитель и знаменатель является многочленом, то для решения неопределенности 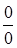необходимо разложить числитель и знаменатель на множители.

Для квадратного трехчлена можно воспользоваться следующей формулой:

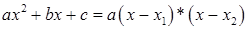
Пример 4

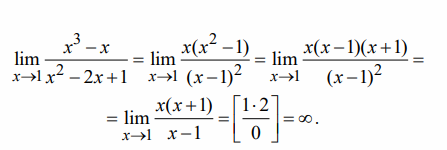
Первый замечательный предел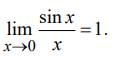

Пример 5

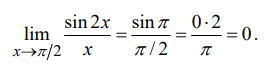НЕ первый замечательный предел

Пример 6

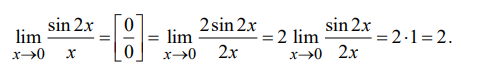
Обычно для добавления недостающей части для возможности применения первого замечательного предела домножаем и числитель и знаменатель, на то чего не хватает.

Второй замечательный предел

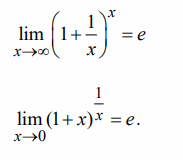
Второй замечательный предел применяется, когда возникает неопределенность вида .

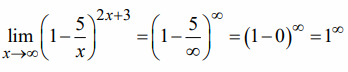
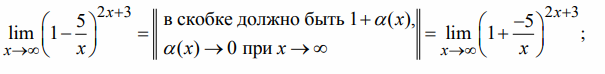
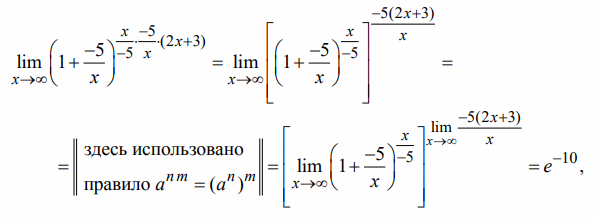
НЕПРЕРЫВНОСТЬ ФУНКИИ

Односторонние пределы

Классификация точек разрыва