
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лемма о перпендикулярности двух параллельных прямых
Перпендикулярность прямых и плоскостей
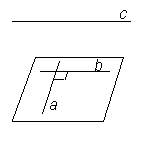
Две прямые в пространстве называются перпендикулярными, если угол между ними 900.
Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.
 α
α
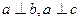 а и b – пересекающиеся прямые
а и с – скрещивающиеся прямые
а и b – пересекающиеся прямые
а и с – скрещивающиеся прямые
| Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
 α
Если
α
Если  , то , то 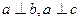 , , 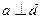 и т. д.
Прямые b, c, d лежат в плоскости α. и т. д.
Прямые b, c, d лежат в плоскости α.
|
Лемма о перпендикулярности двух параллельных прямых
третьей прямой
| Лемма | Если одна из двух параллельных прямых, перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой ( | |
|
Α
Если | Теорема. Если две прямые перпендикулярны плоскости, то они параллельны.
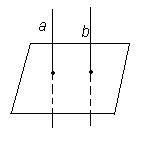 α
Если
α
Если 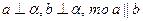
| |
Признак перпендикулярности прямой и плоскости
Теорема. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Теорема о прямой, перпендикулярной плоскости
Через точку пространства проходит прямая, перпендикулярная данной плоскости, и притом только одна.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
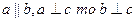 ).
). 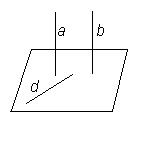 Теорема. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
Теорема. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости. 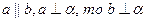 .
.