Контакты

Случайная статья

- это общее решение дифференциального уравнения.

Дифференциальные уравнения.

1. Решить дифференциальное уравнение:

Возможны два случая, когда в явном виде есть 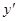, и когда в примере есть 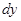и . Пример (1) - это первый случай. Начинаем с того, что представляем .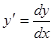

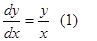
Теперь мы должны перенести в числитель.

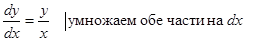
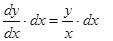
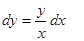теперь смотрим, где стоит 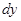и , все функции с переменной 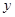должны быть там, где .

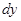А все функции с переменной 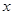должны быть там, где .

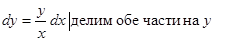
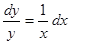интегрируем обе части данного равенства

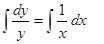
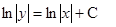переменную С можно обозначить как 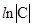. Это делается в тем примерах, где с обеих сторон стоят натуральные логарифмы.

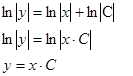
- это общее решение дифференциального уравнения.

2.

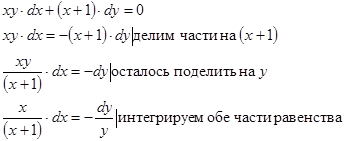
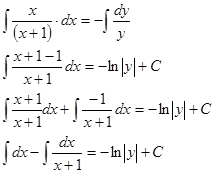
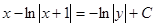
Мы нашли интегралы, получено решение дифференциального уравнения. Выражать 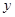через 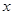не нужно.

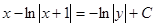- это уже ответ.

Решить самостоятельно:

3.

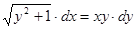
4.

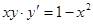
5.

6.

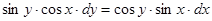
7.

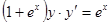
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.