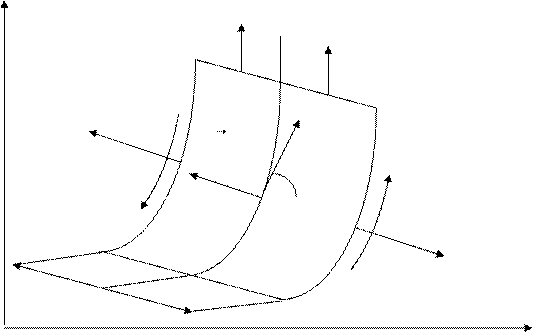
Линии разрыва.. Как и в случае пластического кручения стержня, в плоском деформированном состоянии могут быть линии разрыва напряжений.. Выделим в теле элемент шириныδ. На него действуют напряженияσt+,σt−, σ+n ,σ−n , и

Линии разрыва.

Как и в случае пластического кручения стержня, в плоском деформированном состоянии могут быть линии разрыва напряжений.

Y σ t− L

σ _t⁺

t τ _tn⁻ n β _σ⁻_n τ _tn⁺

δ _σ⁺_n

Рис (12. 1) X

Выделим в теле элемент шириныδ. На него действуют напряженияσ t+, σ t−, σ +n, σ − n, и т. д. (см. Рис (12. 1)). Устремимδ к нулю; получается линия – линия разрыва

напряжений L. Рассматривая условия равновесия выделенного элемента при стремленииδ к нулю аналогично задаче о стержне, получаем соотношения для

напряжений на разрыве: .

Распишем напряжения согласно формулам (9. 2):

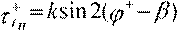
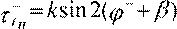
гдеβ - угол поворота системы координатtnотносительно системы XY. Здесь как и ранее символами «+» и «-» обозначаются величины по разные стороны от разрыва.

Условие неразрывности τ _tn⁺=τ _tn⁻даёт: − 2(_ϕ⁺− β ) =П+ 2(_ϕ⁻− β ),

откуда: β =1/2((фи++П/4)+(фи- +П/4)) (10. 3)

Углы фи⁺+П/4 и фи^- +П/4 задают направление характеристик по разные стороны линии L, следовательно, линия разрыва напряжений есть биссектриса угла между характеристиками. Такой же результат был получен и в случае пластического кручения стержня.